
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
$y+120^0=180^0$
$y=180^0-120^0=60^0$
$t=60^0$ (hai góc đối đỉnh)
$z=120^0$ (hai góc so le trong)
$x=60^0$ (hai góc đồng vị)
b. Hình mờ quá không nhìn được bạn ạ.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{8}}=\dfrac{b}{\dfrac{1}{9}}=\dfrac{c}{\dfrac{1}{10}}=\dfrac{a+b+c}{\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}}=\dfrac{121}{\dfrac{121}{360}}=360\)
Do đó: a=45; b=40; c=36

a: Xét ΔMIN vuông tại I và ΔMIP vuông tại I có
MN=MP
MI chung
Do đó: ΔMIN=ΔMIP
b: Xét ΔMKI vuông tại K và ΔMEI vuông tại E có
MI chung
\(\widehat{KMI}=\widehat{EMI}\)
Do đó: ΔMKI=ΔMEI
Suy ra: MK=ME
c: Xét ΔMNP có MK/MN=ME/MP
nên KE//NP

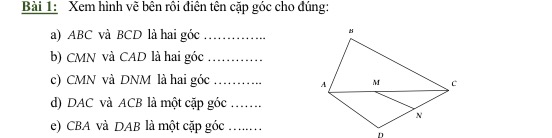
a) Trong cùng phía
b) đồng vị
c) so le trong
d) so le trong
e) trong cùng phía

\(\dfrac{\dfrac{1}{15}}{2x}=\dfrac{75}{4.5}\)
\(\Leftrightarrow2x=\dfrac{1}{250}\)
hay \(x=\dfrac{1}{500}\)

Bài 4:
a: Xét ΔBDC vuông tại D có \(BC^2=BD^2+DC^2\)
nên BC=10(cm)
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{EAC}\) chung
Do đó: ΔABD=ΔACE
c: Ta có: ΔABD=ΔACE
nên AD=AE
hay ΔADE cân tại A
Xét ΔABC có
AE/AB=AD/AC
nên DE//BC
d: Xét ΔDBC vuông tại D và ΔDKC vuông tại D có
DB=DK
DC chung
Do đó: ΔDBC=ΔDKC
Suy ra: \(\widehat{DBC}=\widehat{DKC}\left(1\right)\)
Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
EC=DB
Do đó: ΔEBC=ΔDCB
Suy ra: \(\widehat{ECB}=\widehat{DBC}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{ECB}=\widehat{DKC}\)

Gọi gốc là điểm A, chỗ gãy là B, ngọn đã gãy là điểm C
Xét tam giác ABC vuông tại A có: AB = 6m, BC = 16m - 6m = 10m
=> AB2 + AC2 = BC2 (Định lý Py-ta-go)
Thay: 62 + AC2 = 102
36 + AC2 = 100
AC2 = 100 - 36 = 64
AC = 8 (m)
Vậy khoảng cách từ gốc đến ngọn cây bị gãy là 8 mét
Nếu đúng hãy K cho mình nha
Học tốt nhé


Bài 11:
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
=>AM⊥BC
mà a⊥AM
nên a//BC
c: Xét tứ giác AMCN có
AM//CN
AN//MC
Do đó: AMCN là hình bình hành
Suy ra: AM=CN; AN=MC
Xét ΔAMC và ΔCNA có
AM=CN
MC=NA
AC chung
Do đó: ΔAMC=ΔCNA
d: Ta có: AMCN là hình bình hành
Suy ra: AC và MN cắt nhau tại trung điểm của mỗi đường
mà I là trung điểm của AC
nên I là trung điểm của MN


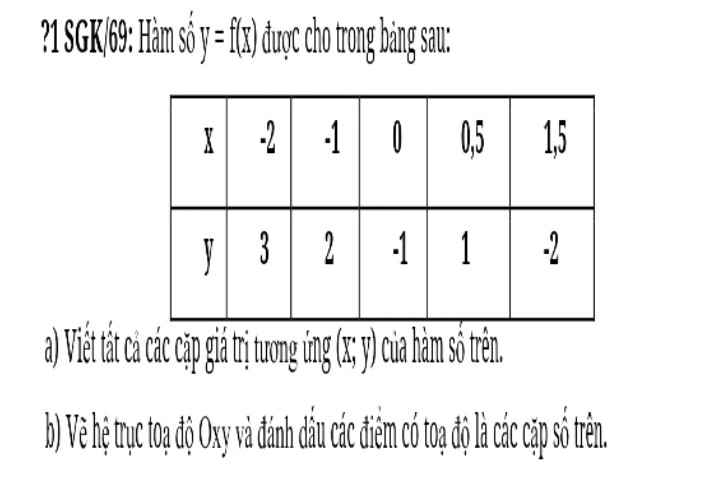


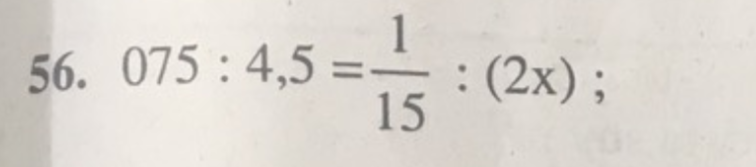 ai làm giúp em với đang gấp lắm ạ
ai làm giúp em với đang gấp lắm ạ


a, góc B1 = góc A1 = \(105^o\)( slt)
mà góc A1 = \(\frac{7}{5}\)A2
=> \(105^o\)=\(\frac{7}{5}\).A2
=>A2 = \(105^o:\frac{7}{5}=75^o\)