
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{3}}=\dfrac{b}{\dfrac{1}{5}}=\dfrac{c}{\dfrac{1}{6}}=\dfrac{a-c}{\dfrac{1}{3}-\dfrac{1}{6}}=\dfrac{10}{\dfrac{1}{6}}=60\)
Do đó: a=20; b=12; c=10


`1)`
`4x-6=0`
`-> 4x=0+6`
`-> 4x=6`
`-> x=6/4=3/2`
Vậy, nghiệm của đa thức là `x=3/2`
`2)`
`5-3x=0`
`-> 3x=5-0`
`-> 3x=5`
`-> x=5/3`
Vậy, nghiệm của đa thức là `x=5/3`
`3)`
`12x+18=0`
`-> 12x=-18`
`-> x=-18/12=-3/2`
Vậy, nghiệm của đa thức là `x=-3/2`
`4)`
`2x^2-4x=0`
`x(2x-4)=0`
`->`\(\left[{}\begin{matrix}x=0\\2x-4=0\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=0\\2x=4\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=0\\x=4\div2\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x={0; 2}`
`5)`
`-x^2+16=0`
`-> -x^2=-16`
`-> x^2=16`
`-> x^2=(+-4)^2`
`-> x=+-4`
Vậy, nghiệm của đa thức là `x={4; -4}`
`6)`
`(4x-3)(5+x)=0`
`->`\(\left[{}\begin{matrix}4x-3=0\\5+x=0\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}4x=3\\x=-5\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=-5\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x={3/4; -5}`
`7)`
`(x^2+3)(3-x)=0`
`->`\(\left[{}\begin{matrix}x^2+3=0\\3-x=0\end{matrix}\right.\)
`->`\(\left[{}\begin{matrix}x^2=-3\text{(không t/m)}\\x=3\end{matrix}\right.\)
Vậy, nghiệm của đa thức là `x=3`
`8)`
`3(x-3)+2(3x-4)=0`
`-> 3x-9+6x-8=0`
`-> 9x-17=0`
`-> 9x=17`
`-> x=17/9`
Vậy, nghiệm của đa thức là `x=17/9`
`9)`
`1/2(2x-4)-0,4(x+5/4)=0`
`-> x-2-0,4x-1/2=0`
`-> 0,6x-2,5=0`
`-> 0,6x=2,5`
`-> x=2,5 \div 0,6`
`-> x=25/6`
Vậy, nghiệm của đa thức là `x=25/6`


+) \(x>2,5\Rightarrow\hept{\begin{cases}x-1,5>0\\2,5-x< 0\end{cases}\Rightarrow}\hept{\begin{cases}\left|x-1,5\right|=x-1,5\\\left|2,5-x\right|=x-2,5\end{cases}}\)
\(\Rightarrow\left(x-1,5\right)-\left(x-2,5\right)=3\Leftrightarrow1=3\left(VN\right)\)
+) \(1,5< x\le2,5\Rightarrow\hept{\begin{cases}x-1,5>0\\2,5-x\ge0\end{cases}\Rightarrow}\hept{\begin{cases}\left|x-1,5\right|=x-1,5\\\left|2,5-x\right|=2,5-x\end{cases}}\)
\(\Rightarrow\left(x-1,5\right)-\left(2,5-x\right)=3\Leftrightarrow2x-1=3\Leftrightarrow x=2\)
+) \(x\le1,5\Rightarrow\hept{\begin{cases}x-1,5\le0\\2,5-x>0\end{cases}\Rightarrow\hept{\begin{cases}\left|x-1,5\right|=1,5-x\\\left|2,5-x\right|=2,5-x\end{cases}}}\)
\(\Rightarrow\left(1,5-x\right)-\left(2,5-x\right)=3\Leftrightarrow-1=3\left(VN\right)\)
Vậy nhận nghiệm \(x=2\)
cảm ơn bạn nhưng mik thấy nếu x=2 thì biểu thức đó sẽ bằng 0 chứ ko phải 3 nên có lẽ bạn sai rồi!



c. \(\left|\dfrac{8}{4}-\left|x-\dfrac{1}{4}\right|\right|-\dfrac{1}{2}=\dfrac{3}{4}\)
\(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{8}{4}-x+\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{8}{4}+x-\dfrac{1}{4}\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left|\dfrac{9}{4}-x\right|-\dfrac{1}{2}=\dfrac{3}{4}\\\left|\dfrac{7}{4}+x\right|-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}\dfrac{9}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\\x=\dfrac{9}{4}-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\\\left[{}\begin{matrix}\dfrac{7}{4}+x-\dfrac{1}{2}=\dfrac{3}{4}\\-\dfrac{7}{4}-x-\dfrac{1}{2}=\dfrac{3}{4}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\end{matrix}\right.\\\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{7}{2}\\x=-3\end{matrix}\right.\)
Ở nơi x=9/4-1/2 là x-9/4-1/2 nha
a. -1,5 + 2x = 2,5
<=> 2x = 2,5 + 1,5
<=> 2x = 4
<=> x = 2
b. \(\dfrac{3}{2}\left(x+5\right)-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{3}{2}x+\dfrac{15}{2}-\dfrac{1}{2}=\dfrac{4}{3}\)
<=> \(\dfrac{9x}{6}+\dfrac{45}{6}-\dfrac{3}{6}=\dfrac{8}{6}\)
<=> 9x + 45 - 3 = 8
<=> 9x = 8 + 3 - 45
<=> 9x = -34
<=> x = \(\dfrac{-34}{9}\)



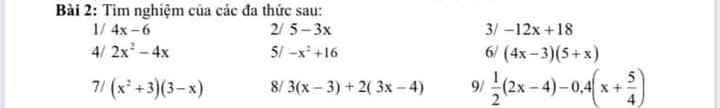 giúp mik với đang vội ạ
giúp mik với đang vội ạ
 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
a) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{2y}{6}=\dfrac{3z}{12}=\dfrac{x+2y-3z}{2+6-12}=\dfrac{-20}{-4}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5.2=10\\y=5.3=15\\z=5.4=20\end{matrix}\right.\)
b) \(7x=3y\Rightarrow\dfrac{x}{3}=\dfrac{y}{7}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=\dfrac{16}{-4}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).3=-12\\y=\left(-4\right).7=-28\end{matrix}\right.\)