
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1
a
\(A=x^2-2x+4=x^2-2x+1+3\\=\left(x-1\right)^2+3\ge3\)
Min A = 3 khi và chỉ khi `x=1`
b
\(B=x^2+4x+5=x^2+4x+4+1\\ =\left(x+2\right)^2+1\ge1\)
Min B = 1 khi và chỉ khi `x=-2`
c
\(C=x^2+3x+4=x^2+3x+\dfrac{9}{4}+\dfrac{7}{4}\\ =\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
Min C = \(\dfrac{7}{4}\) khi và chỉ khi \(x=-\dfrac{3}{2}\)
d
\(D=3x^2-6x+4=3\left(x^2-2x+\dfrac{4}{3}\right)\\ =3\left(x^2-2x+1+\dfrac{1}{3}\right)\\ =3\left(x-1\right)^2+3.\dfrac{1}{3}\ge3.\dfrac{1}{3}\)
Min D = 1 khi và chỉ khi `x=1`

\(a,=x^3+3x^2+3x+1-x^3+4x^2-4x-1\\ =7x^2-x\\ b,=\left[\left(x+1\right)\left(x^2-x+1\right)\right]\left[\left(x-1\right)\left(x^2+x+1\right)\right]\\ =\left(x^3+1\right)\left(x^3-1\right)=x^6-1\\ c,=8a^2+12a^2+6a+1\\ d,=27a^3-54a^2b+36ab^2-8b^3\)

a) Vì D là điềm đối xứng với H qua AB nên AB là đường trung trực của DH
suy ra AH=AD (1)
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE
suy ra AH=AE (2)
Từ (1) và (2) suy ra AD=AE (3)
Mặt khác ^DAB=^BAH; ^HAC=^CAE và ^BAH+^HAC=90*
do đó ^DAB+^BAH+ ^HAC+^CAE=180*
tức là D, A, E thẳng hàng (4)
từ (3) và (4) suy ra D và E đối xứng với nhau qua A.
b) Tam giác DHE có HA là trung tuyến và HA= 1/2 DE
nên tam giác DHE vuông tại H.
c) Tam giác ADB=tam giác AHB (c-c-c)
suy ra ^ADB=^AHB=90*
tương tự có ^AEC=90*
suy ra BD//CE (cùng vuông góc với DE)
nên tứ giác BAEC là hình thang có 2 góc vuông kề cạnh bên DE
nên BAEC là hình thang vuông.
d) Do AB là đường trung trực của DH nên BD=BH (5)
Do AC là đường trung trực của EH nên CE=CH (6)
công vế với vế của (5) và (6) ta có BD+CE=BH+CH
hay BD+CE=BC
k mik nha bn

a) \(=3\left(xy-4\right)\)
b) \(=x^2\left(x-y\right)+4\left(x-y\right)=\left(x-y\right)\left(x^2+4\right)\)
c) \(=x^2-\left(y^2-12y+36\right)=x^2-\left(y-6\right)^2=\left(x-y+6\right)\left(x+y-6\right)\)
d) \(=\left(4p^2-36p+81\right)-25=\left(2p-9\right)^2-25=\left(2p-9-5\right)\left(2p-9+5\right)=4\left(p-7\right)\left(p-2\right)\)

a: \(\widehat{A}=120^0\)
\(\widehat{B}=\widehat{D}=60^0\)


(x-3)^3-(x+3)^3
= x^3 - 3^3 - x^3 + 3^3
= x^3 - x^3 - 9 + 9
= x^3 - x^3
= 0


a, \(A=x\left(2x^2-3-5x^2-x+x\right)=x\left(-3x-3\right)\)\(=-3x\left(x+1\right)\)
b, \(B=3x^2-6x-5x+5x^2-8x^2+24\)\(=-9x+24\)
C, \(C=x\left(2x^4-x^2-4x^4-2x^2+x-2x+6x^2\right)\)\(=x\left(-2x^4+3x^2-x\right)=-2x^5+3x^3-x^2\)
Chúc học tốt !
Lm ko chép lại đề

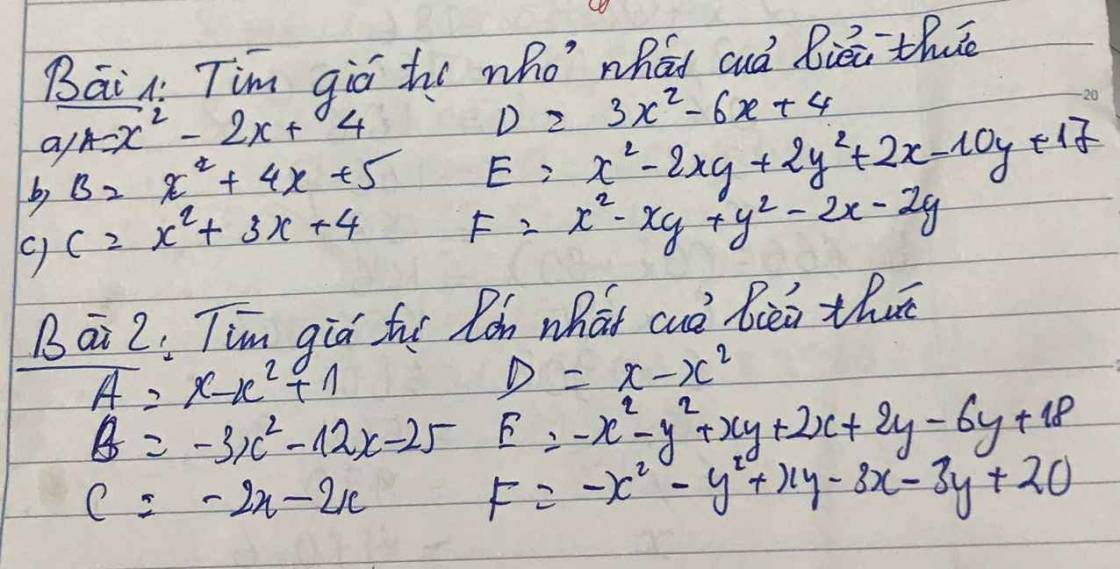


 mn giải giúp em vơi ạ em đang cần gấp cảm ơn
mn giải giúp em vơi ạ em đang cần gấp cảm ơn

3. gọi tử là x
mẫu là x + 8
Nếu thêm vào tử và bớt mẫu:
tử là x+2
mẫu là x+5
Ta có: \(\dfrac{x+2}{x+5}\)=\(\dfrac{3}{4}\)
4(x+2)=3(x+5)
4x + 8 = 3x + 15
x = 7
Tử số là 7
Mẫu số là x+8= 7+8= 15
Vậy phân số ban đầu l: \(\dfrac{7}{15}\)
2. \(\dfrac{3\left(x-2\right)}{6}\)- \(\dfrac{4}{6}\)> \(\dfrac{6x}{6}\)-\(\dfrac{6}{6}\)
<=> 3x - 6 - 4> 6x - 6
<=> 3x - 6 - 4 - 6x + 6> 0
<=> -3x -4 > 0
<=> -3x > 4
<=> x < \(\dfrac{-4}{3}\)
S= {x/x <\(\dfrac{-4}{3}\)}
trục số bạn tự vẽ giúp mình nhé