
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3. gọi tử là x
mẫu là x + 8
Nếu thêm vào tử và bớt mẫu:
tử là x+2
mẫu là x+5
Ta có: \(\dfrac{x+2}{x+5}\)=\(\dfrac{3}{4}\)
4(x+2)=3(x+5)
4x + 8 = 3x + 15
x = 7
Tử số là 7
Mẫu số là x+8= 7+8= 15
Vậy phân số ban đầu l: \(\dfrac{7}{15}\)
2. \(\dfrac{3\left(x-2\right)}{6}\)- \(\dfrac{4}{6}\)> \(\dfrac{6x}{6}\)-\(\dfrac{6}{6}\)
<=> 3x - 6 - 4> 6x - 6
<=> 3x - 6 - 4 - 6x + 6> 0
<=> -3x -4 > 0
<=> -3x > 4
<=> x < \(\dfrac{-4}{3}\)
S= {x/x <\(\dfrac{-4}{3}\)}
trục số bạn tự vẽ giúp mình nhé

a: \(\widehat{A}=120^0\)
\(\widehat{B}=\widehat{D}=60^0\)



\(a,=x^3+3x^2+3x+1-x^3+4x^2-4x-1\\ =7x^2-x\\ b,=\left[\left(x+1\right)\left(x^2-x+1\right)\right]\left[\left(x-1\right)\left(x^2+x+1\right)\right]\\ =\left(x^3+1\right)\left(x^3-1\right)=x^6-1\\ c,=8a^2+12a^2+6a+1\\ d,=27a^3-54a^2b+36ab^2-8b^3\)

e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)

\(a,=\dfrac{x^3+2x}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2}{x^2+x+1}-\dfrac{1}{x-1}=\dfrac{x^3+2x+2x-2-\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3+3}{\left(x^2+x+1\right)}\)
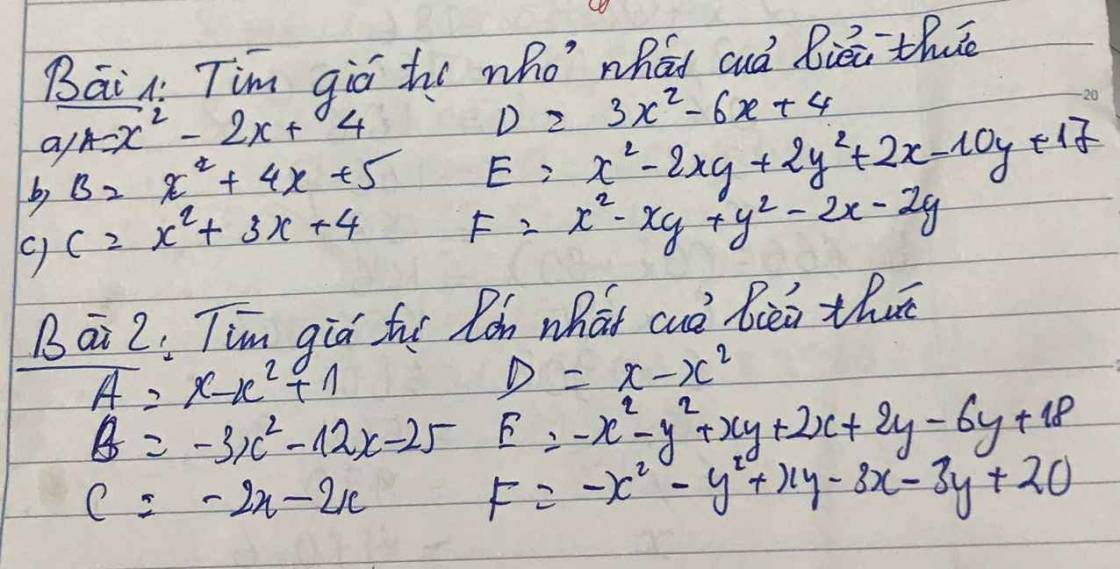


 mn giải giúp em vơi ạ em đang cần gấp cảm ơn
mn giải giúp em vơi ạ em đang cần gấp cảm ơn

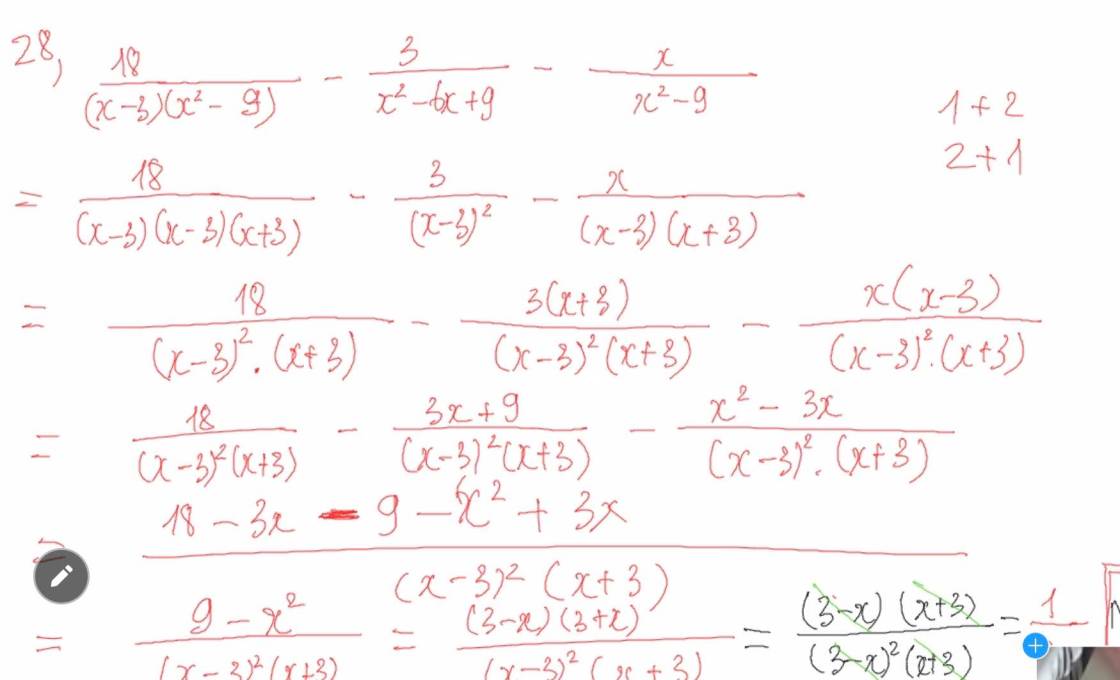
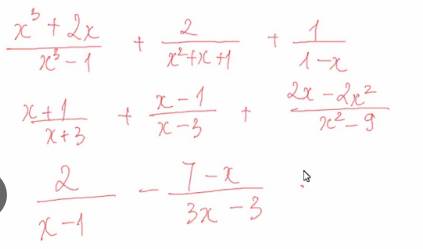
1
a
\(A=x^2-2x+4=x^2-2x+1+3\\=\left(x-1\right)^2+3\ge3\)
Min A = 3 khi và chỉ khi `x=1`
b
\(B=x^2+4x+5=x^2+4x+4+1\\ =\left(x+2\right)^2+1\ge1\)
Min B = 1 khi và chỉ khi `x=-2`
c
\(C=x^2+3x+4=x^2+3x+\dfrac{9}{4}+\dfrac{7}{4}\\ =\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
Min C = \(\dfrac{7}{4}\) khi và chỉ khi \(x=-\dfrac{3}{2}\)
d
\(D=3x^2-6x+4=3\left(x^2-2x+\dfrac{4}{3}\right)\\ =3\left(x^2-2x+1+\dfrac{1}{3}\right)\\ =3\left(x-1\right)^2+3.\dfrac{1}{3}\ge3.\dfrac{1}{3}\)
Min D = 1 khi và chỉ khi `x=1`