
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)


giả sử n^2+n+2=k^2=> k^2>n^2<==>k>n (1)
ta có n^2+n-2=k^2-4
<==>(n-1)(n+2)=(k-2)(k+2) (2)
@ nếu n=1 , k=2, đúng
@ nếu n khác 1
ta có n+2<k+2 (từ (1))
==> để (2) xẩy ra thì: n-1>k-2
mà từ (1) ta có k-1>n-1
nên: k-1>n-1>k-2
do k-1 và k-2 hai hai số tự nhiên liên tiếp nên không thể tồn tại số tự nhiên nằm giữa chúng (n-1)
vậy chỉ có n=1 là nghiệm!

a) \(\sqrt{4x}+\sqrt{\dfrac{x}{4}}+\dfrac{1}{2}\sqrt{49x}=6\left(x\ge0\right)\)
\(\Rightarrow2\sqrt{x}+\dfrac{1}{2}\sqrt{x}+\dfrac{7}{2}\sqrt{x}=6\Rightarrow6\sqrt{x}=6\Rightarrow\sqrt{x}=1\Rightarrow x=1\)
b) ĐKXĐ: \(x\ge\dfrac{1}{2}\)
\(\sqrt{18x-9}-0,5\sqrt{2x-1}+\dfrac{1}{2}\sqrt{25\left(2x-1\right)}+\sqrt{49\left(2x-1\right)}=24\)
\(\Rightarrow\sqrt{9\left(2x-1\right)}-0,5\sqrt{2x-1}+\dfrac{5}{2}\sqrt{2x-1}+7\sqrt{2x-1}=24\)
\(\Rightarrow3\sqrt{2x-1}-0,5\sqrt{2x-1}+\dfrac{5}{2}\sqrt{2x-1}+7\sqrt{2x-1}=24\)
\(\Rightarrow12\sqrt{2x-1}=24\Rightarrow\sqrt{2x-1}=2\Rightarrow2x-1=4\Rightarrow x=\dfrac{5}{2}\)
c) \(\sqrt{x^2-2x+1}-7=0\Rightarrow\sqrt{\left(x-1\right)^2}=7\Rightarrow\left|x-1\right|=7\)
\(\Rightarrow\left[{}\begin{matrix}x-1=7\\x-1=-7\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=8\\x=-6\end{matrix}\right.\)
d) \(\dfrac{1}{2}\sqrt{\dfrac{49x}{x+2}}-3\sqrt{\dfrac{x}{4x+8}}-2\sqrt{\dfrac{x}{x+2}}-\sqrt{5}=0\left(\dfrac{x}{x+2}\ge0,x\ne-2\right)\)
\(\Rightarrow\dfrac{7}{2}\sqrt{\dfrac{x}{x+2}}-3\sqrt{\dfrac{x}{4\left(x+2\right)}}-2\sqrt{\dfrac{x}{x+2}}=\sqrt{5}\)
\(\Rightarrow\dfrac{7}{2}\sqrt{\dfrac{x}{x+2}}-\dfrac{3}{2}\sqrt{\dfrac{x}{x+2}}-2\sqrt{\dfrac{x}{x+2}}=\sqrt{5}\)
\(\Rightarrow0=\sqrt{5}\) (vô lý) \(\Rightarrow\) pt vô nghiệm
a) \(\sqrt{4x}+\sqrt{\dfrac{x}{4}}+\dfrac{1}{2}\sqrt{49x}=6\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\2\sqrt{x}+\dfrac{\sqrt{x}}{2}+\dfrac{7}{2}\sqrt{x}=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt{x}\left(2+\dfrac{1}{2}+\dfrac{7}{2}\right)=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\6\sqrt{x}=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt{x}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x=1\end{matrix}\right.\) \(\Leftrightarrow x=1\)
Vậy \(S=\left\{1\right\}\)
b) \(\sqrt{18x-9}-0.5\sqrt{2x-1}+\dfrac{1}{2}\sqrt{25\left(2x-1\right)}+\sqrt{49\left(2x-1\right)}=24\)
\(\Leftrightarrow3\sqrt{2x-1}-0,5\sqrt{2x-1}+\dfrac{5}{2}\sqrt{2x-1}+7\sqrt{2x-1}=24\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-1\ge0\\\sqrt{2x-1}\left(3-0.5+\dfrac{5}{2}+7\right)=49\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\12\sqrt{2x-1}=24\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\\sqrt{2x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\2x-1=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\x=\dfrac{5}{2}\end{matrix}\right.\) \(\Leftrightarrow x=\dfrac{5}{2}\)
Vậy \(S=\left\{\dfrac{5}{2}\right\}\)
c) \(\sqrt{x^2-2x+1}-7=0\) (*)
Ta có \(x^2-2x+1=\left(x-1\right)^2\ge0\forall x\) \(\Rightarrow\sqrt{x^2-2x+1}\ge0\forall x\)
(*) \(\Leftrightarrow\sqrt{\left(x-1\right)^2}-7=0\)
\(\Leftrightarrow\left|x-1\right|-7=0\)
\(\Leftrightarrow x-1-7=0\)
\(\Leftrightarrow x=8\)
Vậy \(S=\left\{8\right\}\)
\(\)d) \(\dfrac{1}{2}\sqrt{\dfrac{49x}{x+2}}-3\sqrt{\dfrac{x}{4x+8}}-2\sqrt{\dfrac{x}{x+2}}-\sqrt{5}=0\) (**)
\(\Leftrightarrow\dfrac{7}{2}\sqrt{\dfrac{x}{x+2}}-\dfrac{3}{2}\sqrt{\dfrac{x}{x+2}}-2\sqrt{\dfrac{x}{x+2}}=\sqrt{5}\)
ĐKXĐ: \(\dfrac{x}{x+2}\ge0\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x+2>0\end{matrix}\right.\\\left\{{}\begin{matrix}x\le0\\x+2< 0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x>-2\end{matrix}\right.\\\left\{{}\begin{matrix}x\le0\\x< -2\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge0\\x< -2\end{matrix}\right.\)
(**) \(\Leftrightarrow\sqrt{\dfrac{x}{x+2}}\left(\dfrac{7}{2}-\dfrac{3}{2}-2\right)=\sqrt{5}\)
\(\Leftrightarrow0\sqrt{\dfrac{x}{x+2}}=\sqrt{5}\)
\(\Leftrightarrow0=\sqrt{5}\) ( vô lý )
Vậy phương trình trên vô nghiệm

a. ĐKXĐ: $x\in\mathbb{R}$
PT \(\Rightarrow \left\{\begin{matrix} 2-x\geq 0\\ x^2+x+2=(3-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ x^2+x+2=x^2-6x+9\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 2\\ 7x=7\end{matrix}\right.\Leftrightarrow x=1\)
b. ĐKXĐ: $x\geq -1$
PT $\Leftrightarrow (x^2-1)+\sqrt{x+1}=0$
$\Leftrightarrow (x-1)(x+1)+\sqrt{x+1}=0$
$\Leftrightarrow \sqrt{x+1}[(x-1)\sqrt{x+1}+1]=0$
$\Leftrightarrow \sqrt{x+1}=0$ hoặc $(x-1)\sqrt{x+1}+1=0$
Nếu $\sqrt{x+1}=0$
$\Leftrightarrow x=-1$ (tm)
Nếu $(x-1)\sqrt{x+1}+1=0$
$\Leftrightarrow (x-1)\sqrt{x+1}=-1$
$\Rightarrow (x-1)^2(x+1)=1$
$\Leftrightarrow x^3-x^2-x=0$
$\Leftrightarrow x(x^2-x-1)=0$
$\Leftrightarrow x=0$ hoặc $x^2-x-1=0$
$\Leftrightarrow x=0$ hoặc $x=\frac{1\pm \sqrt{5}}{2}$
Kết hợp đkxđ suy ra $x=0; -1; \frac{1\pm \sqrt{5}}{2}$
c. ĐKXĐ: $x\geq 2$
PT $\Leftrightarrow \sqrt{(x-2)(x+2)}-2\sqrt{x-2}=0$
$\Leftrightarrow \sqrt{x-2}(\sqrt{x+2}-2)=0$
$\Leftrightarrow \sqrt{x-2}=0$ hoặc $\sqrt{x+2}-2=0$
$\Leftrightarrow x=2$ (thỏa mãn)
d. ĐKXĐ: $x\geq 3$ hoặc $x\leq -4$
PT \(\Rightarrow \left\{\begin{matrix} 8-x\geq 0\\ x^2+x-12=(8-x)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ x^2+x-12=x^2-16x+64\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\leq 8\\ 17x=76\end{matrix}\right.\Leftrightarrow x=\frac{76}{17}\) (tm)

5:
a: góc ACB=1/2*180=90 độ
Xét ΔAKH vuông tại K và ΔACB vuông tại A có
góc KAH chung
=>ΔAKH đồng dạng với ΔACB
b: Xét ΔADC và ΔBEC có
AD=BE
góc DAC=góc EBC
AC=BC
=>ΔADC=ΔBEC
=>DC=EC
=>ΔDEC cân tại C
góc CAB=45 độ
=>góc CDE=góc CAB=45 độ
=>ΔCDE vuông cân tại C

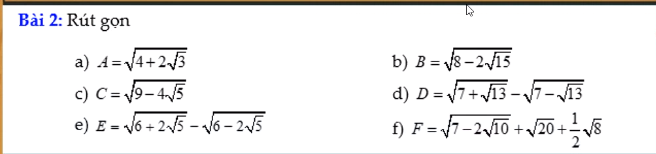 giúp mik với cả 2 bài nha
giúp mik với cả 2 bài nha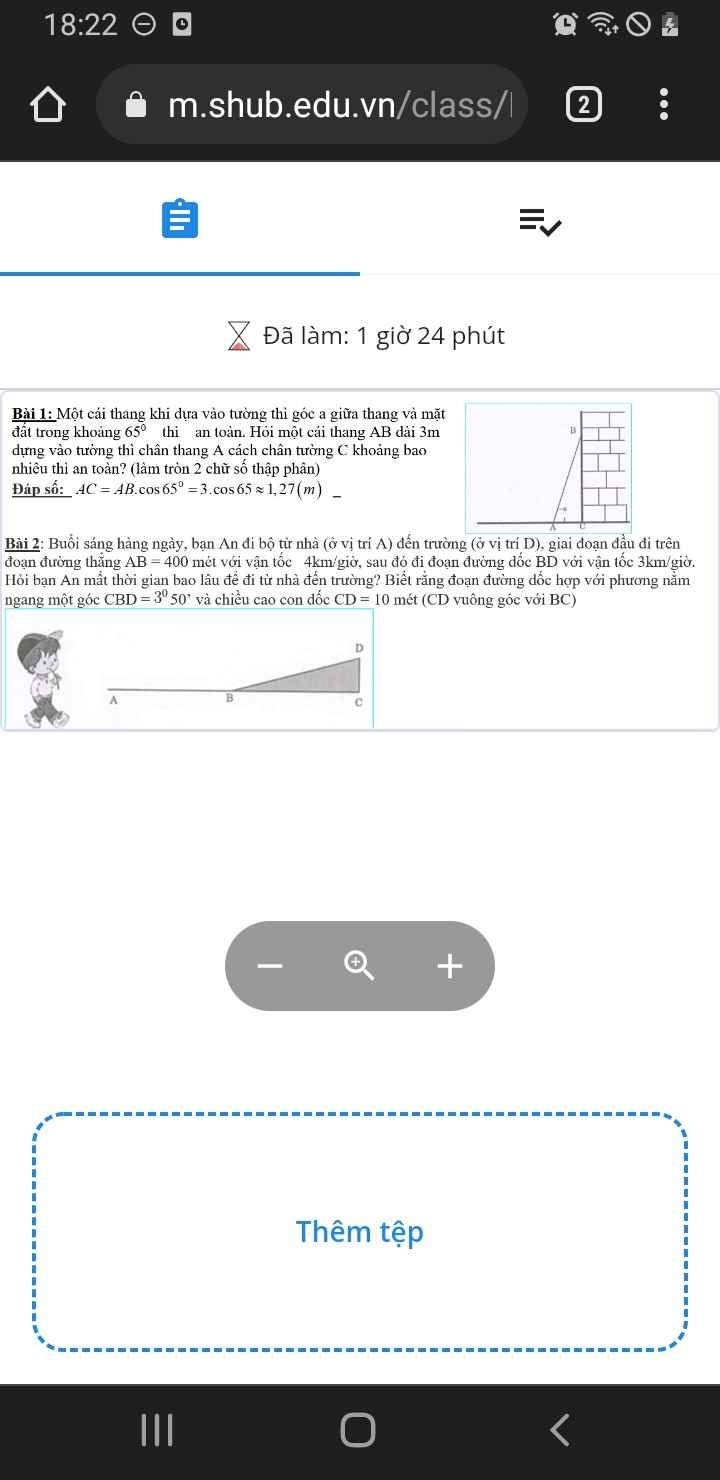






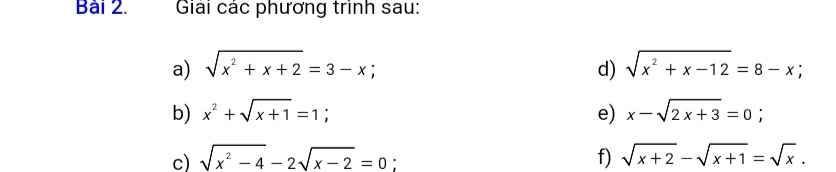

a) \(A=\sqrt{6-2\sqrt{5}}=\sqrt{\left(\sqrt{5}-1\right)^2}=\left|\sqrt{5}-1\right|=\sqrt{5}-1\)
b) \(B=\sqrt{4-\sqrt{12}}=\sqrt{\left(\sqrt{3}-1\right)^2}=\left|\sqrt{3}-1\right|=\sqrt{3}-1\)
c) \(C=\sqrt{19-8\sqrt{3}}=\sqrt{\left(4-\sqrt{3}\right)^2}=\left|4-\sqrt{3}\right|=4-\sqrt{3}\)
d) \(D=\sqrt{5-2\sqrt{6}}=\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}=\left|\sqrt{3}-\sqrt{2}\right|=\sqrt{3}-\sqrt{2}\)
a) \(A=\sqrt{6-2\sqrt{5}}=\sqrt{5}-1\)
b) \(B=\sqrt{4-\sqrt{12}}=\sqrt{3}-1\)
c) \(C=\sqrt{19-8\sqrt{3}}=4-\sqrt{3}\)
d) \(D=\sqrt{5-2\sqrt{6}}=\sqrt{3}-\sqrt{2}\)