
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Coi ban đầu có n dãy ghế ( \(n\in N\)*; n < 250 , \(n\inƯ\left(250\right)\))
Ban đầu mỗi dãy có số chỗ ngồi là : \(\frac{250}{n}\) ( chỗ )
Do có 308 người dự họp, btc kê thêm 3 dãy ghế, mỗi dãy thêm một chỗ ngồi nên ta có phương trình :
\(\left(\frac{250}{n}+1\right)\left(n+3\right)=308\)
Bạn giải PT là ra n = 25 (TMĐK) và mỗi dãy ghế có 250 / 25 = 10 ( chỗ ngồi ).


Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)

Bài 2:
b: Gọi (d'): y=ax+b
Vì (d')//(D) nên a=2
hay y=2x+b
Thay x=-1 và y=2 vào y=2x+b, ta được:
\(2\cdot\left(-1\right)+b=2\)
\(\Leftrightarrow b=0\)
Vậy: y=2x

\(\left\{{}\begin{matrix}2x+3\sqrt{y-2}=5\\3x-2\sqrt{y-2}=1\end{matrix}\right.\). (ĐK: \(y\geq 2\))
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y-2}=1\end{matrix}\right.\Leftrightarrow x=1;y=3\)

a, do MA và MB là 2 tiếp tuyến của (O) (gt)
-> MA vg với AO, MB vg với OB -> góc MAO = góc MBO = 90 độ
Xét tg AMBO có góc MAO + góc MBO = 180 độ; góc MBO và góc MAO là 2 góc đối -> tg AMBO là TGNT
b, Xét (O) có:
- góc MAC là góc tạo bởi tia tiếp tuyến và dây chắn cung AC
- góc CDA là góc nt chắn cung AC
=> góc MAC = góc CDA
tự cm 2 tam giác đồng dạng (gg)
c,do tg MAC ~ tg MDA (cmt)
=> MA/MD = MC/MA (cạnh t/ư)
=> \(MA^2=MD.MC\) (1)
Do MA và MB là 2 tiếp tuyến của (O) nên MO là phân giác △AOB
Mà △AOB cân tại O (2 cạnh là 2 bk (O))
=> MO là đường cao △AOB => OH là đường cao △AOB => OH vg với AB ( OH vg với AH )
Xét △AOM vuông tại A có AH là đg cao
=> \(MA^2=MH.MO\) (HTL) (2)
Từ (1) (2) => MD.MC=MH.MO (đpcm)

3: Ta có: A=B|x-4|
\(\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}-5}:\dfrac{1}{\sqrt{x}-5}=\left|x-4\right|\)
\(\Leftrightarrow\left|x-4\right|=\sqrt{x}-2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=\sqrt{x}-2\left(x\ge4;x\ne25\right)\\x-4=2-\sqrt{x}\left(0< x< 4\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-\sqrt{x}-2=0\\x+\sqrt{x}-6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=4\left(loại\right)\end{matrix}\right.\)
1: Thay x=9 vào A, ta được:
\(A=\dfrac{3-2}{3-5}=\dfrac{-1}{-2}=\dfrac{1}{2}\)
2: Ta có: \(B=\dfrac{3}{\sqrt{x}+5}+\dfrac{20-2\sqrt{x}}{x-25}\)
\(=\dfrac{3\sqrt{x}-15+20-2\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\)
\(=\dfrac{1}{\sqrt{x}-5}\)


 Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 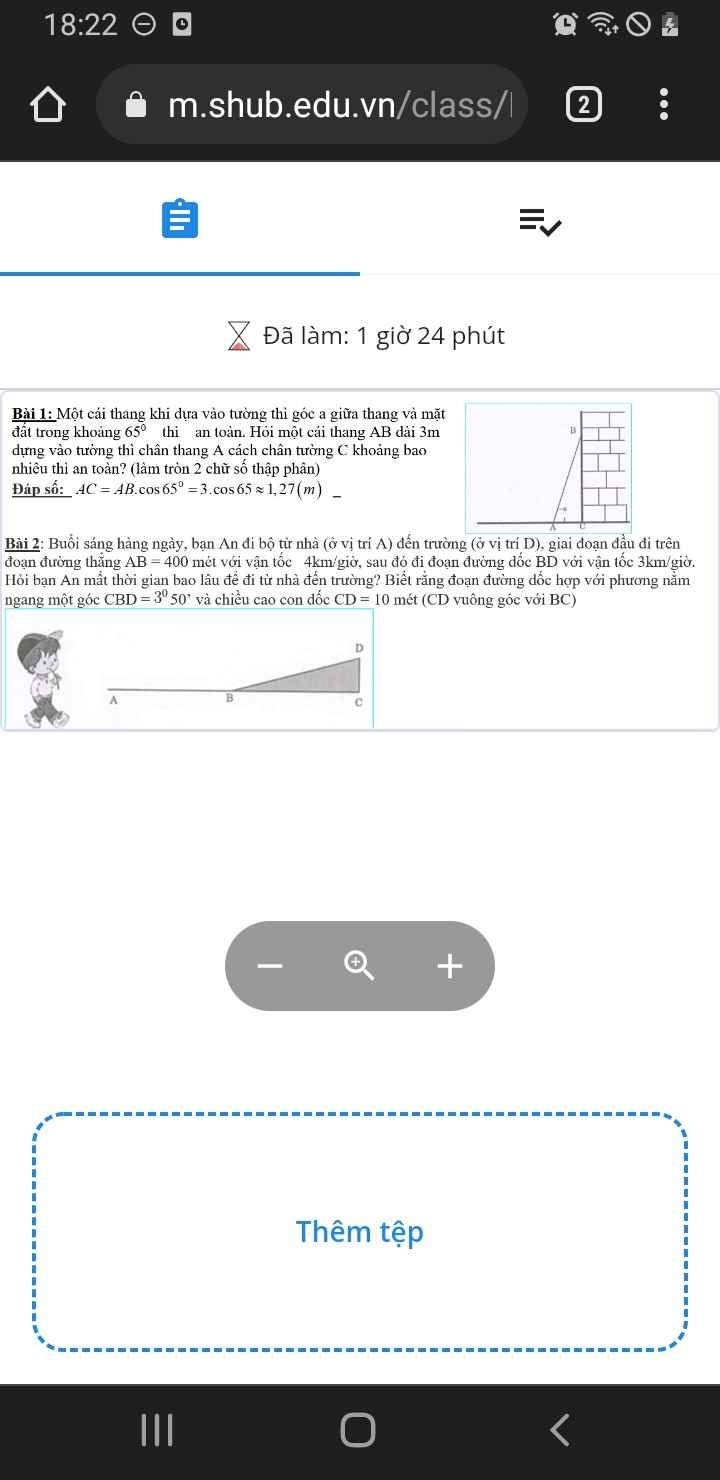


 giúp mik với mik cần gấp
giúp mik với mik cần gấp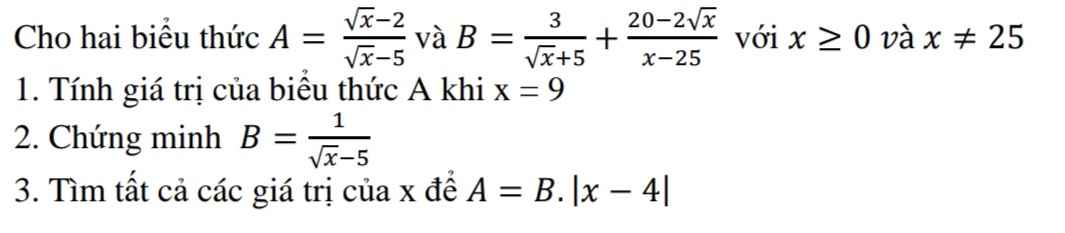

a, Ta có : \(\sqrt{4+4\sqrt{3}+3=a+b\sqrt{3}}\)
\(\Leftrightarrow\sqrt{7+4\sqrt{3}=a+b\sqrt{3}}\)
-> a = 7 ; b = 4
Thay vào ta được \(a^2+b^2=49+16=65\)
b, Ta có : \(=\sqrt{3}+1+\sqrt{3}-1=a\sqrt{3}\)
\(\Leftrightarrow2\sqrt{3}=a\sqrt{3}\Rightarrow a=2\)( tmđk \(a\in Z\))
Thay vào ta được \(2.2\sqrt{3}=4\sqrt{3}\)