K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
10 tháng 4 2023
Để phương trình có 2 nghiệm phân biệt thì:
\(\Delta>0\\ \Leftrightarrow\left(-5\right)^2-4.1.\left(m+4\right)>0\\ \Leftrightarrow25-4m-16>0\\\Leftrightarrow9-4m>0\\ \Leftrightarrow m< \dfrac{9}{4}\)
Theo viét:
\(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=m+4\end{matrix}\right.\)
c,
\(\left|x_1-x_2\right|=3\\ \Leftrightarrow\left(x_1-x_2\right)^2=9\\ \Leftrightarrow x_1^2-2x_1x_2+x_2^2=9\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=9\\ \Leftrightarrow5^2-4\left(m+4\right)=9\\ \Leftrightarrow25-4m-16=9\\ \Leftrightarrow m=0\left(nhận\right)\)
d.
\(\left|x_1\right|+\left|x_2\right|=4\\ \)
Xét trường hợp 1: hai nghiệm đều dương:
ta có:
\(x_1+x_2=4\)
5 = 4 (vô lý)
Loại trường hợp này.
Xét trường hợp 2: hai nghiệm đều âm, tương tự ta loại trường hợp này.
Xét trường hợp 3:
\(x_1< 0< x_2\)
=> \(x_2-x_1=4\)
<=> \(x_2+x_1-2x_1=4\)
=> \(5-2x_1=4\)
=> \(x_1=\dfrac{1}{2}\)
\(x_2< 0< x_1\)
\(x_1-x_2=4\\ \Leftrightarrow x_1+x_2-2x_2=4\\ \Leftrightarrow5-2x_2=4\\ \Rightarrow x_2=\dfrac{1}{2}\)
Có: \(x_1x_2=m+4\\\)
<=> \(\dfrac{1}{2}.\dfrac{1}{2}=m+4\)
=> m = -3,75 (nhận)
e.
Theo viét và theo đề ta có:
\(\left\{{}\begin{matrix}3x_1+4x_2=6\left(1\right)\\x_1+x_2=5\left(2\right)\\x_1x_2=m+4\left(3\right)\end{matrix}\right.\)
Từ (1) có \(x_1=\dfrac{6-4x_2}{3}=2-\dfrac{4}{3}x_2\) (x)
Thế (x) vào (2) được \(2-\dfrac{4}{3}x_2+x_2=5\)
=> \(x_2=-9\) (xx)
Thế (xx) vào (1) được \(3x_1+4.\left(-9\right)=6\)
=> \(x_1=14\) (xxx)
Thế (xx) và (xxx) vào (3) được:
\(14.\left(-9\right)=m+4\)
=> m = -130 (nhận)
h.
\(x_1\left(1-3x_2\right)+x_2\left(1-3x_1\right)=m^2-23\)
<=> \(x_1-3x_1x_2+x_2-3x_1x_2=m^2-23\)
<=> \(x_1+x_2-6x_1x_2=m^2-23\)
<=> \(5-6.\left(m+4\right)=m^2-23\)
<=> \(5-6m-20-m^2+23=0\)
<=> \(-m^2-6m+8=0\)
\(\Delta=\left(-6\right)^2-4.\left(-1\right).8=68\)
\(m_1=\dfrac{6+\sqrt{68}}{2.\left(-1\right)}=-3-\sqrt{17}\left(nhận\right)\)
\(m_2=\dfrac{6-\sqrt{68}}{2.\left(-1\right)}=-3+\sqrt{17}\left(nhận\right)\)
☕T.Lam
Mình không chắc chắn ở câu d, mình lên đây để ôn bài thi tiện thể giúp được bạn phần nào.
TT
2
31 tháng 10 2021
b: Xét ΔAHC vuông tại H có
\(AH^2+HC^2=AC^2\)
nên \(AC^2-HC^2=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AH^2=AN\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AC=AC^2-HC^2\)
25 tháng 12 2021
1: Xét ΔABE vuông tại B và ΔADC vuông tại D có
\(\widehat{AEB}=\widehat{ACD}\)
Do đó: ΔABE∼ΔADC
Suy ra: \(\dfrac{AB}{AD}=\dfrac{AE}{AC}\)
hay \(AB\cdot AC=AE\cdot AD\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
\(\sqrt{9-3\sqrt{5}}-\sqrt{9+3\sqrt{5}}=\dfrac{1}{\sqrt{2}}\left(\sqrt{18-6\sqrt{5}}-\sqrt{18+6\sqrt{5}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{15}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{15}+\sqrt{3}\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{15}-\sqrt{3}-\sqrt{15}-\sqrt{3}\right)=-\dfrac{2\sqrt{3}}{\sqrt{2}}=-\sqrt{6}\)
\(\sqrt{4-\sqrt{15}}+\sqrt{4+\sqrt{15}}-2\sqrt{3-\sqrt{5}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{15}}+\sqrt{8+2\sqrt{15}}-2\sqrt{6-2\sqrt{5}}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}-2\sqrt{\left(\sqrt{5}-1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{5}-\sqrt{3}+\sqrt{5}+\sqrt{3}-2\left(\sqrt{5}-1\right)\right)\)
\(=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
24 tháng 8 2021
k: Ta có: \(\sqrt{9-3\sqrt{5}}-\sqrt{9+3\sqrt{5}}\)
\(=\dfrac{\sqrt{18-6\sqrt{5}}-\sqrt{18+6\sqrt{5}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{15}-\sqrt{3}-\sqrt{15}-\sqrt{3}}{\sqrt{2}}\)
\(=-\sqrt{6}\)
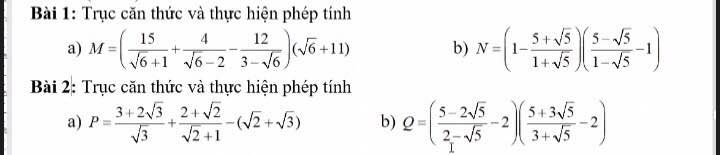
\(B=cos^212+sin^2\left(90-78\right)+cos^21+sin^2\left(90-89\right)\)
\(=cos^212+sin^212+cos^21+sin^21=1+1=2\)
\(C=sin^23+sin^215+cos^2\left(90-75\right)+cos^2\left(90-87\right)\)
\(=sin^23+cos^23+sin^215+cos^215=1+1=2\)
\(E=\dfrac{tan64}{cot26}-1=\dfrac{tan64}{tan\left(90-26\right)}-1=\dfrac{tan64}{tan64}-1=1-1=0\)