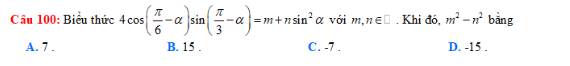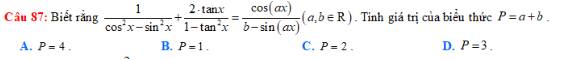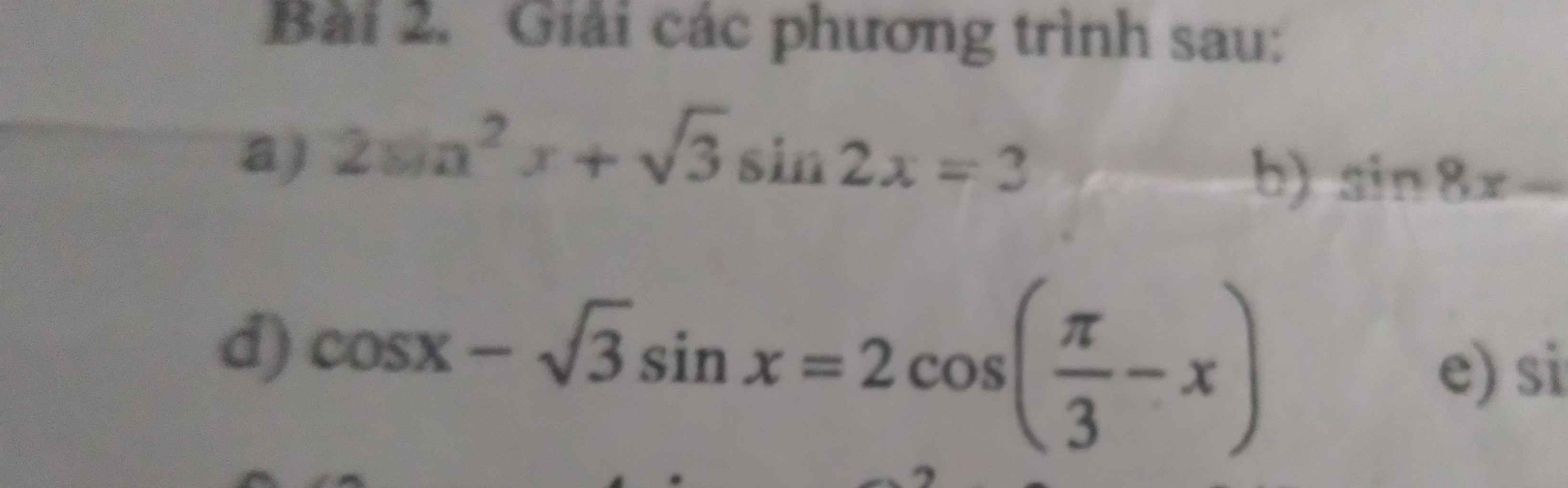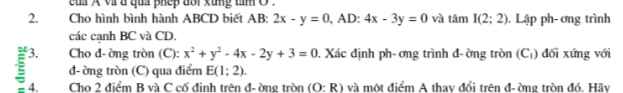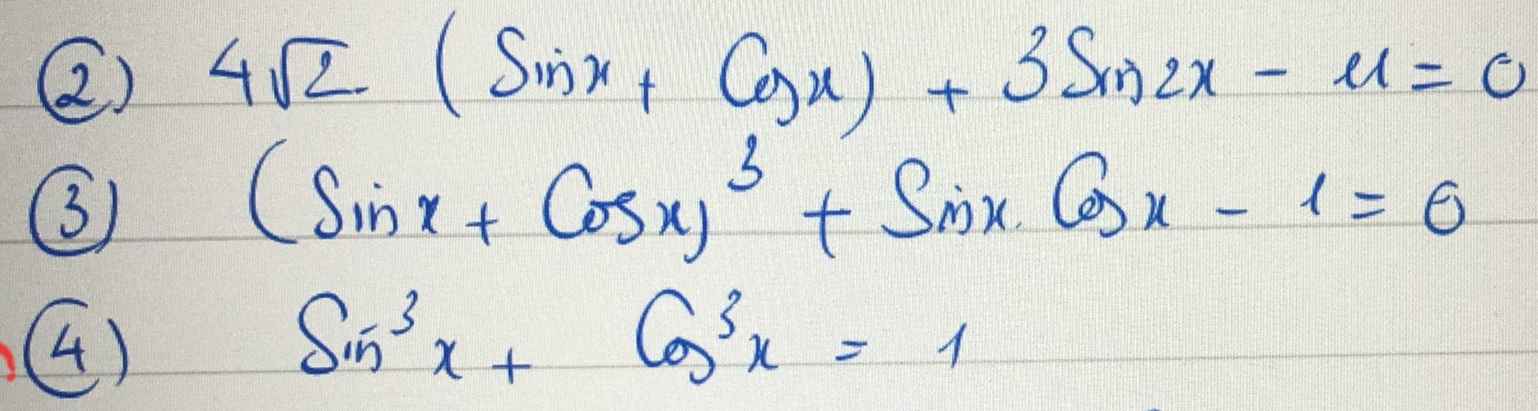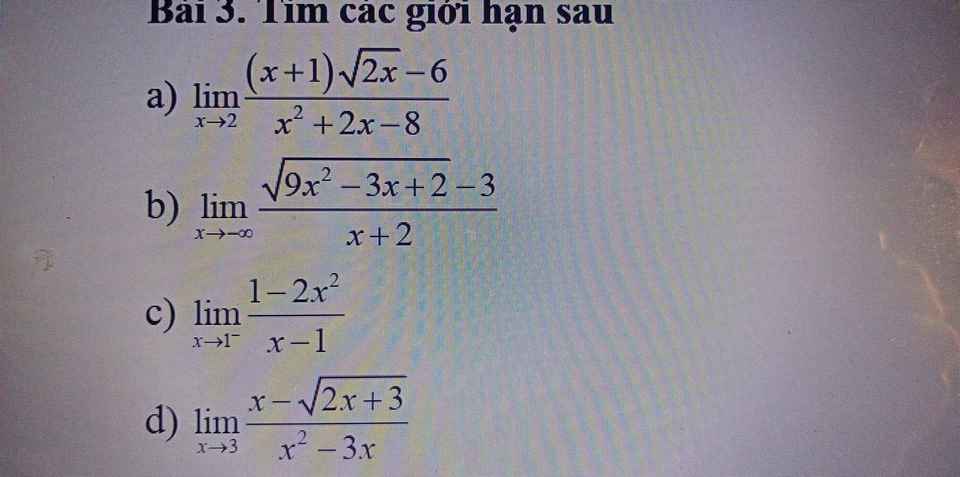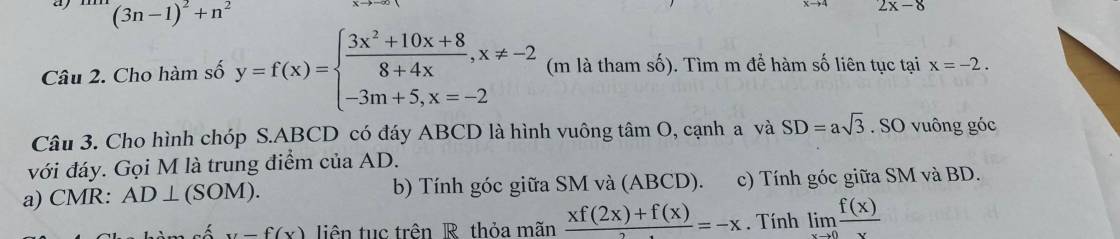K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BA
1
21 tháng 7 2023
4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7
BA
1
20 tháng 7 2023
Ta có:
\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)
\(\Rightarrow P=a+b=2+1=3\)
HP
1 tháng 9 2021
a, \(2sin^2x+\sqrt{3}sin2x=3\)
\(\Leftrightarrow-\left(1-2sin^2x\right)+\sqrt{3}sin2x=2\)
\(\Leftrightarrow\sqrt{3}sin2x-cos2x=2\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
HP
1 tháng 9 2021
d, \(cosx-\sqrt{3}sinx=2cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow-2sin\dfrac{\pi}{3}.sinx=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2021
Đường tròn (C) có pt:
\(\left(x-2\right)^2+\left(y-1\right)^2=2\Rightarrow\) (C) tâm \(I\left(2;1\right)\) bán kính \(R=\sqrt{2}\)
\(\left(C_1\right)\) đối xứng (C) qua E \(\Rightarrow\left(C_1\right)\) có tâm \(I_1\) là ảnh của I qua phép đối xứng tâm I và bán kính \(R_1=R=\sqrt{2}\)
\(\left\{{}\begin{matrix}x_{I_1}=2x_E-x_I=0\\y_{I1}=2y_E-y_I=3\end{matrix}\right.\)
Phương trình: \(x^2+\left(y-3\right)^2=2\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2022
a.
\(\lim\limits_{x\rightarrow2}\dfrac{x\sqrt{2x}+\sqrt{2x}-6}{x^2+2x-8}=\lim\limits_{x\rightarrow2}\dfrac{\left(x\sqrt{2x}-4\right)+\left(\sqrt{2x}-2\right)}{\left(x-2\right)\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2x^3-16}{x\sqrt{2x}+4}+\dfrac{2x-4}{\sqrt{2x}+2}}{\left(x-2\right)\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2\left(x-2\right)\left(x^2+2x+4\right)}{x\sqrt{2x}+4}+\dfrac{2\left(x-2\right)}{\sqrt{2x}+2}}{\left(x-2\right)\left(x+4\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\dfrac{2\left(x^2+2x+4\right)}{x\sqrt{2x}+4}+\dfrac{2}{\sqrt{2x}+2}}{x+4}\)
\(=\dfrac{\dfrac{2\left(2^2+2.2+4\right)}{2\sqrt{4}+4}+\dfrac{2}{\sqrt{4}+2}}{2+4}\)
\(=...\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2022
b.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{9x^2-3x+2}-3}{x+2}=\lim\limits_{x\rightarrow-\infty}\dfrac{\left|x\right|\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-3}{x+2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-x\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-3}{x+2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{x\left(-\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-\dfrac{3}{x}\right)}{x\left(1+\dfrac{2}{x}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{9-\dfrac{3}{x}+\dfrac{2}{x^2}}-\dfrac{3}{x}}{1+\dfrac{2}{x}}\)
\(=\dfrac{-\sqrt{9-0+0}-0}{1+0}=...\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2023
b.
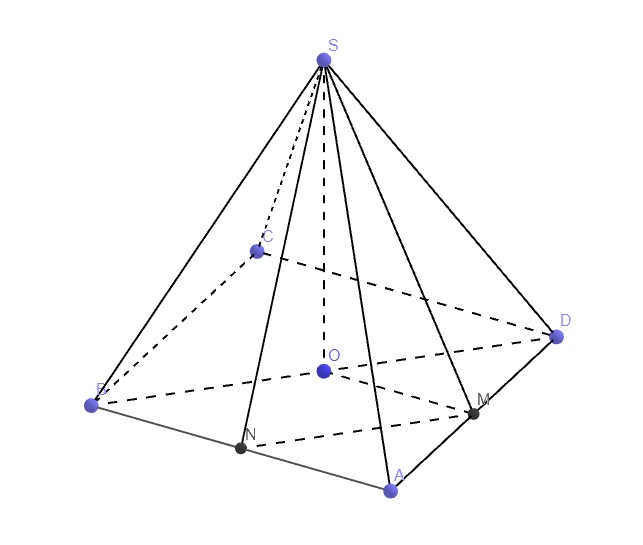
\(SO\perp\left(ABCD\right)\Rightarrow OM\) là hình chiếu vuông gốc của SM lên (ABCD)
\(\Rightarrow\widehat{SMO}\) là góc giữa SM và (ABCD)
\(BD=a\sqrt{2}\Rightarrow SO=\sqrt{SD^2-OD^2}=\sqrt{3a^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a\sqrt{10}}{2}\)
\(OM=\dfrac{1}{2}AB=\dfrac{a}{2}\)
\(\Rightarrow tan\widehat{SMO}=\sqrt{10}\Rightarrow\widehat{SMO}=...\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(SM;BD\right)}=\widehat{\left(SM;MN\right)}=\widehat{SMN}\)
\(OM=ON\Rightarrow SN=SM=\sqrt{SO^2+OM^2}=\dfrac{a\sqrt{11}}{2}\)
Định lý hàm cos:
\(cos\widehat{SMN}=\dfrac{SM^2+MN^2-SN^2}{2SM.MN}=\dfrac{\sqrt{22}}{22}\Rightarrow\widehat{SMN}=...\)
