
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4:
a: =>2/5x+7/20-2/20=1/10
=>2/5x+5/20=1/10
=>2/5x=1/10-1/4=4/40-10/40=-6/40=-3/20
=>x=-3/20:2/5=-3/20*5/2=-15/40=-3/8
b: 3/2-1/2x=-1/3+3=8/3
=>1/2x=3/2-8/3=9/6-16/6=-7/6
=>x=-7/6*2=-7/3
c: 15/8-1/8:(1/4x-0,5)=5/4
=>1/8:(1/4x-1/2)=15/8-5/4=15/8-10/8=5/8
=>1/4x-1/2=1/8:5/8=1/5
=>1/4x=1/5+1/2=7/10
=>x=7/10*4=28/10=2,8
d: \(\Leftrightarrow\left[\left(x+\dfrac{1}{2}\right)^3-\dfrac{5}{4}\right]=\dfrac{11}{4}-\dfrac{5}{8}=\dfrac{22-5}{8}=\dfrac{17}{8}\)
=>\(\left(x+\dfrac{1}{2}\right)^3=\dfrac{17}{8}+\dfrac{5}{4}=\dfrac{27}{8}\)
=>x+1/2=3/2
=>x=1


Bài 1
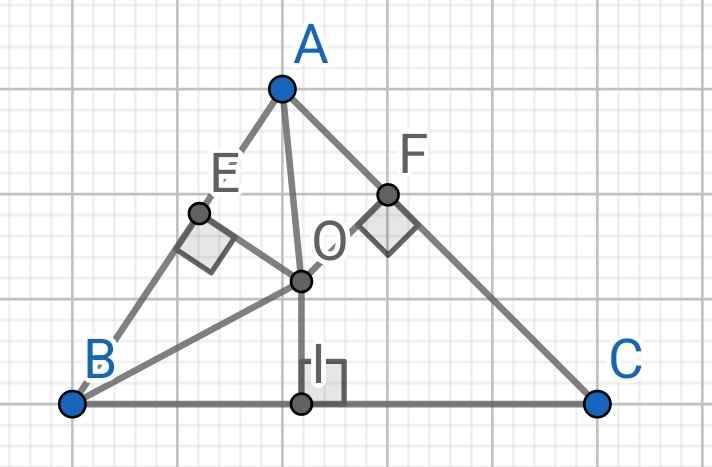 Do BO là tia phân giác của ∠ABC (gt)
Do BO là tia phân giác của ∠ABC (gt)
⇒ ∠OBE = ∠OBI
Do AO là tia phân giác của ∠BAC (gt)
⇒ ∠OAE = ∠OAF
Xét hai tam giác vuông: ∆OAE và ∆OAF có:
OA chung
∠OAE = ∠OAF (cmt)
⇒ ∆OAE = ∆OAF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng) (1)
Xét hai tam giác vuông: ∆OBE và ∆OBI có:
OB chung
∠OBE = ∠OBI (cmt)
⇒ ∆OBE = ∆OBI (cạnh huyền - góc nhọn)
⇒ OE = OI (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ OE = OF = OI
Bài 2
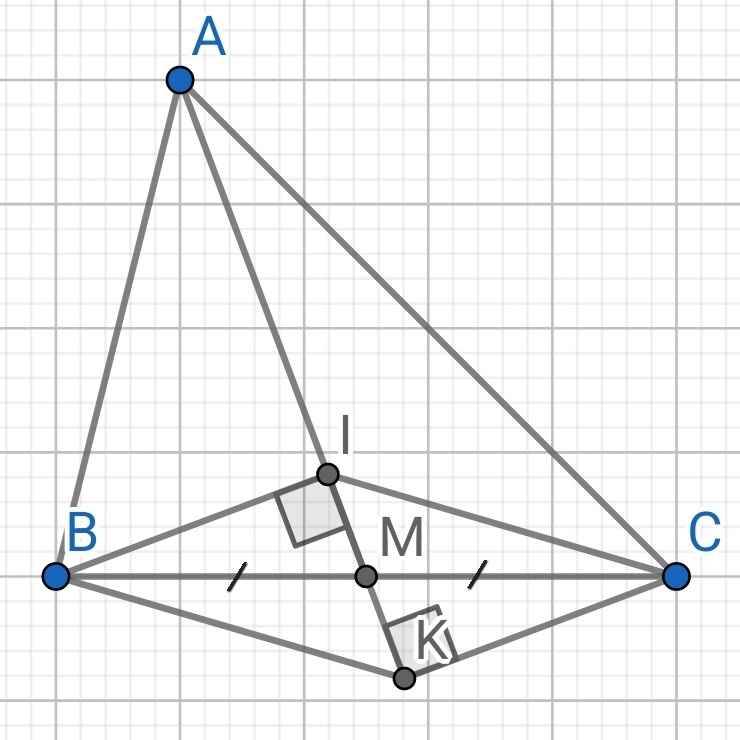 a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
BM = CM (gt)
∠BMI = ∠CMK (đối đỉnh)
⇒ ∆BMI = ∆CMK (cạnh huyền - góc nhọn)
⇒ BI = CK (hai canhk tương ứn
b) Do ∆BMI = ∆CMK (cmt)
⇒ MI = MK (hai cạnh tương ứng)
Xét ∆BMK và ∆CMI có:
MK = MI (cmt)
∠BMK = ∠CMI (đối đỉnh)
BM = CM (gt)
⇒ ∆BMK = ∆CMI (c-g-c)
⇒ ∠MBK = ∠MCI (hai góc tương ứng)
Mà ∠MBK và ∠MCI là hai góc so le trong)
⇒ BK // CI

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
EB chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔABE=ΔDBE
b: Xét ΔAEF vuông tại A và ΔDEC vuông tại D có
EA=ED
\(\widehat{AEF}=\widehat{DEC}\)
Do đó: ΔAEF=ΔDEC
Suy ra: AF=DC
c:ta có: BA+AF=BF
BD+DC=BC
mà BA=BD
và AF=DC
nên BF=BC
=>ΔBFC cân tại B
mà BE là đường phân giác
nên BE là đường cao


Hình 1:
a: Ta có: AC//BD
AB\(\perp\)AC
Do đó: BD\(\perp\)AB

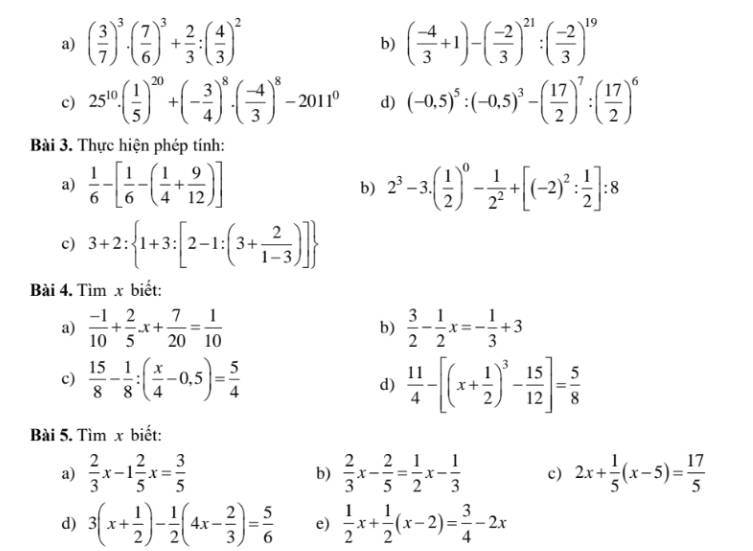
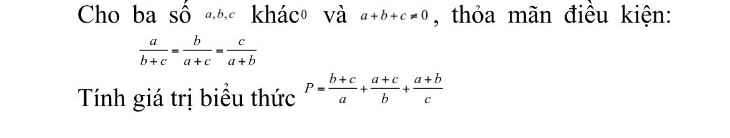




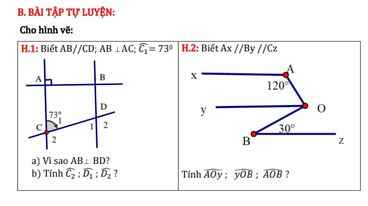 giúp mik giải bài toán hình 7 này với ạ
giúp mik giải bài toán hình 7 này với ạ