K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 7 2021
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC, ta được:
\(BH^2=HA\cdot HC\)
\(\Leftrightarrow BH^2=2\cdot6=12\)
hay \(BH=2\sqrt{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBHA vuông tại H, ta được:
\(BA^2=BH^2+HA^2\)
\(\Leftrightarrow AB^2=\left(2\sqrt{3}\right)^2+2^2=12+4=16\)
hay BA=4(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BA^2+BC^2\)
\(\Leftrightarrow BC^2=8^2-4^2=48\)
hay \(BC=4\sqrt{3}\left(cm\right)\)
13 tháng 7 2021
b) Xét ΔABC vuông tại B có
\(\sin\widehat{A}=\dfrac{BC}{CA}=\dfrac{4\sqrt{3}}{8}=\dfrac{\sqrt{3}}{2}\)
\(\cos\widehat{A}=\dfrac{BA}{CA}=\dfrac{4}{8}=\dfrac{1}{2}\)
Giúp mik câu 3 bài 1 với ạ
31 tháng 1 2023
1: Khi x=9 thì \(A=\dfrac{9+2+4}{3-2}=15\)
2: \(B=\dfrac{3x-4-x+4-x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
3: \(P=\dfrac{A}{B}=\dfrac{x+\sqrt{x}+4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
\(=\dfrac{x+\sqrt{x}+4}{\sqrt{x}+1}=\sqrt{x}+\dfrac{4}{\sqrt{x}+1}\)
\(=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}-1\)
=>\(P>=2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}-1=2\cdot2-1=3\)
Dấu = xảy ra khi (căn x+1)^2=4
=>căn x+1=2
=>x=1
15 tháng 8 2023
1: ĐKXĐ: x>=0 và căn x-2<>0
=>x>=0 và x<>4
2: \(=\sqrt{\left(\sqrt{15}+2\right)^2}-\sqrt{\left(\sqrt{15}-2\right)^2}\)
\(=\sqrt{15}+2-\sqrt{15}+2\)
=4
3: \(=\sqrt{\left(\sqrt{5}+\sqrt{2}\right)^2}-2\sqrt{5}-\dfrac{1}{2}\cdot2\sqrt{2}\)
\(=\sqrt{5}+\sqrt{2}-2\sqrt{5}-\sqrt{2}=-\sqrt{5}\)
20 tháng 6 2023
1:
AC=căn 5^2-3^2=4cm
BH=AB^2/BC=1,8cm
CH=5-1,8=3,2cm
AH=3*4/5=2,4cm
2:
ΔCBA vuông tại B có tan 40=BC/BA
=>BC/10=tan40
=>BC=8,39(m)
ΔCBD vuông tại B có tan D=BC/BD
=>BD=8,39/tan35=11,98(m)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 11 2021
Gọi A là giao điểm của (d) với (d1)
\(\Rightarrow\) Tọa độ A thỏa mãn: \(\left\{{}\begin{matrix}y=-x+2\\y=3x+1\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{1}{4};\dfrac{7}{4}\right)\)
Thay tọa độ A vào pt (d2) ta được:
\(\dfrac{7}{4}=2.\dfrac{1}{4}+2\Rightarrow\dfrac{7}{4}=\dfrac{5}{2}\) (ko thỏa mãn)
Vậy 3 đường thẳng nói trên ko đồng quy (đề bài sai)
29 tháng 8 2021
Ta có: \(\dfrac{AB}{AC}=\dfrac{2}{3}\). Gọi \(AB=2x\left(cm\right),AC=3x\left(cm\right)\)
Áp dụng định lý Pytago trong tam giác vuông ABC:
\(BC^2=AB^2+AC^2=4x^2+9x^2=13x^2\)
\(\Rightarrow BC=\sqrt{13}x\)
Xét tam giác ABC vuông tại A có đường cao AH:
\(AH.BC=AB.AC\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow6\sqrt{13}x=6x^2\)
\(\Rightarrow x^2-\sqrt{13}x=0\)
Vì x > 0
\(\Rightarrow x=\sqrt{13}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}AB=2x=2\sqrt{13}\left(cm\right)\\AC=3x=3\sqrt{13}\left(cm\right)\\BC=\sqrt{13}x=13\left(cm\right)\end{matrix}\right.\)
29 tháng 8 2021
Ta có: \(\dfrac{AB}{AC}=\dfrac{2}{3}\)
nên \(\dfrac{HB}{HC}=\dfrac{4}{9}\)
\(\Leftrightarrow HB=\dfrac{4}{9}HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{4}{9}=36\)
\(\Leftrightarrow HC^2=16\)
\(\Leftrightarrow HC=4\left(cm\right)\)
\(\Leftrightarrow HB=9\left(cm\right)\)
Ta có: BH+HC=BC
nên BC=4+9=13(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\sqrt{13}\left(cm\right)\\AC=3\sqrt{13}\left(cm\right)\end{matrix}\right.\)
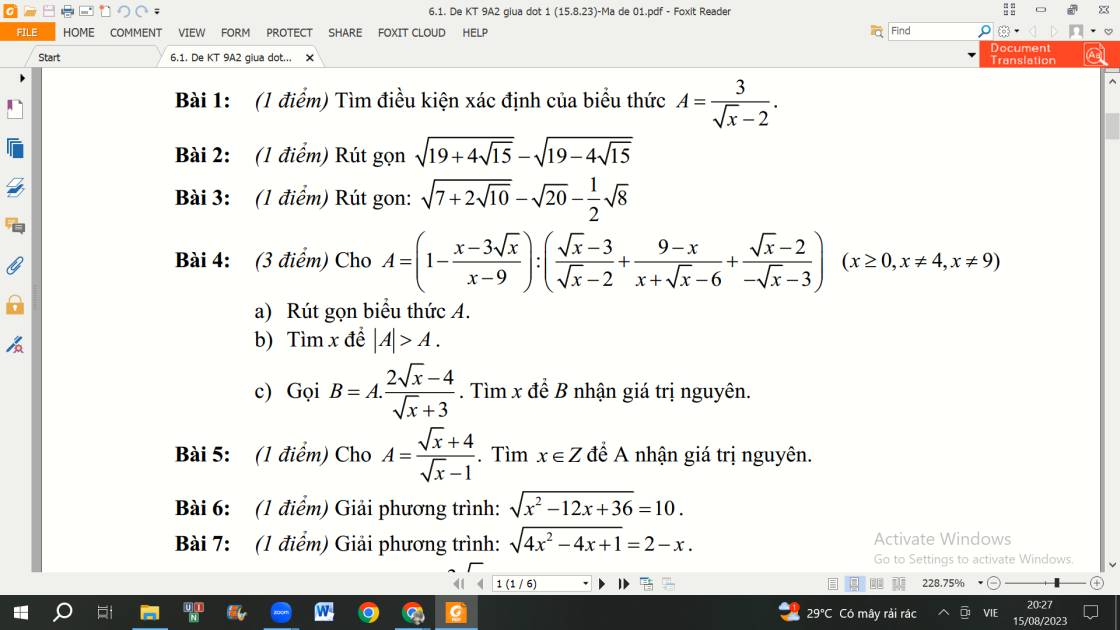
Bài 1:
a: Khi x=36 thì \(B=\left(\dfrac{6+1}{6-2}-1\right)=\left(\dfrac{7}{3}-1\right)=\dfrac{4}{3}\)
b: \(A=\dfrac{\sqrt{x}+\sqrt{x}-2-2\sqrt{x}-4}{x-4}=\dfrac{-2\sqrt{x}-6}{x-4}\)