
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: Ta có: \(\widehat{DBE}=\widehat{ABE}\)
mà \(\widehat{ABE}=\widehat{DEB}\)
nên \(\widehat{DBE}=\widehat{DEB}\)

Bài 1
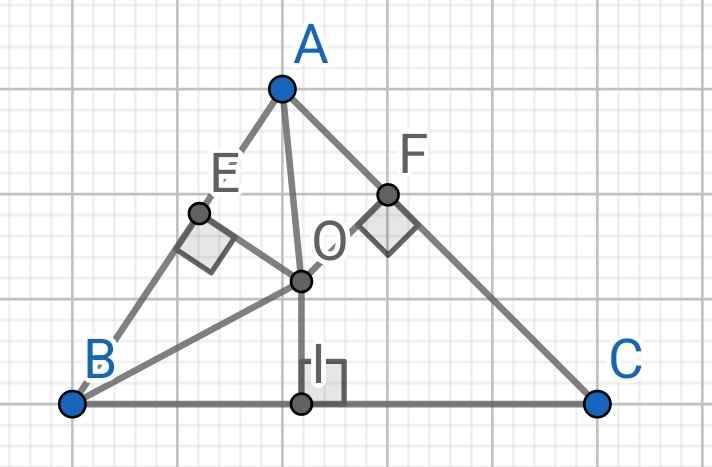 Do BO là tia phân giác của ∠ABC (gt)
Do BO là tia phân giác của ∠ABC (gt)
⇒ ∠OBE = ∠OBI
Do AO là tia phân giác của ∠BAC (gt)
⇒ ∠OAE = ∠OAF
Xét hai tam giác vuông: ∆OAE và ∆OAF có:
OA chung
∠OAE = ∠OAF (cmt)
⇒ ∆OAE = ∆OAF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng) (1)
Xét hai tam giác vuông: ∆OBE và ∆OBI có:
OB chung
∠OBE = ∠OBI (cmt)
⇒ ∆OBE = ∆OBI (cạnh huyền - góc nhọn)
⇒ OE = OI (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ OE = OF = OI
Bài 2
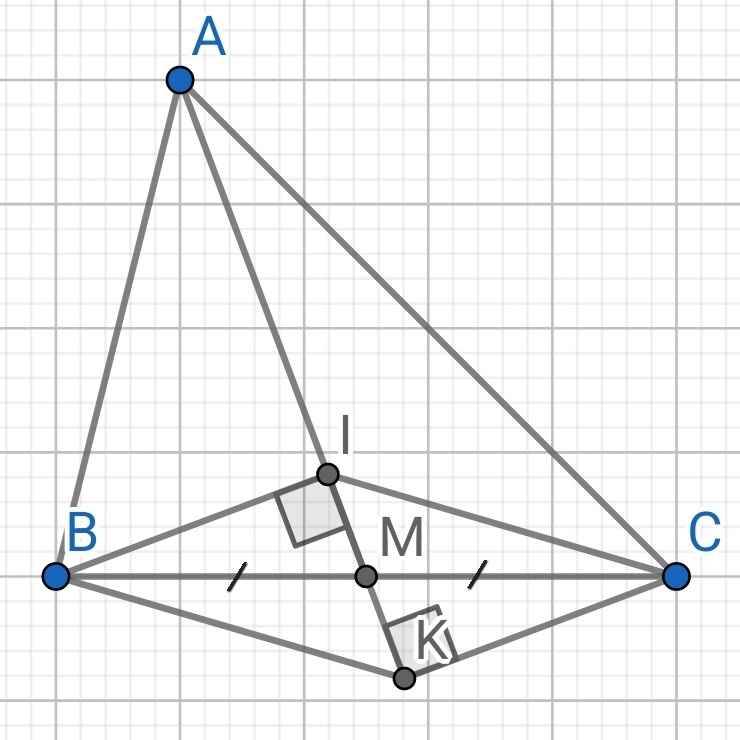 a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
BM = CM (gt)
∠BMI = ∠CMK (đối đỉnh)
⇒ ∆BMI = ∆CMK (cạnh huyền - góc nhọn)
⇒ BI = CK (hai canhk tương ứn
b) Do ∆BMI = ∆CMK (cmt)
⇒ MI = MK (hai cạnh tương ứng)
Xét ∆BMK và ∆CMI có:
MK = MI (cmt)
∠BMK = ∠CMI (đối đỉnh)
BM = CM (gt)
⇒ ∆BMK = ∆CMI (c-g-c)
⇒ ∠MBK = ∠MCI (hai góc tương ứng)
Mà ∠MBK và ∠MCI là hai góc so le trong)
⇒ BK // CI

1B:
i: áp dụng tính chất của dãy tỉ só bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{x+y}{4+5}=\dfrac{54}{9}=6\)
Do đó: x=24; y=30
ii: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{3x-2y}{3\cdot4-2\cdot5}=\dfrac{8}{2}=4\)
Do đó: x=16; y=20
iii: đặt x/4=y/5=k
=>x=4k; y=5k
xy=80 nên \(20k^2=80\)
=>\(k^2=4\)
TH1: k=2
=>x=8; y=10
TH2: k=-2
=>x=-8; y=-10
a thịn ái đồ lun làm toán bất biến giữa dòng box vạn biến
a rep cmt e zesi:>

bài 2
h)
\(5^x+5^x.5^3=630\)
\(5^x\left(1+5^3\right)=630\)
\(5^x.126=630\)
\(5^x=5\)
x=1
bài 2
b) \(2/3\)\(.(-5/3)+11/3.-5/3\)
\(=(2/3+11/3).(-5/3)\)
\(=-65/9\)

b: Xét tứ giác ABCK có
M là trung điểm của AC
M là trung điểm của BK
Do đó: ABCK là hình bình hành
Suy ra: BC=AK

\(3,\\ a,\dfrac{2011}{2010}=1+\dfrac{1}{2010};\dfrac{3011}{3010}=1+\dfrac{1}{3010}\\ \dfrac{1}{2010}>\dfrac{1}{3010}\left(2010< 3010\right)\Rightarrow\dfrac{2011}{2010}>\dfrac{3011}{3010}\\ b,A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ A=\left(1+\dfrac{1}{3}+...+\dfrac{1}{99}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)\\ A=\left(1+\dfrac{1}{3}+...+\dfrac{1}{99}\right)+\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)-2\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)\\ A=\left(1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{50}\right)\\ A=\dfrac{1}{51}+\dfrac{1}{52}+....+\dfrac{1}{100}=B\)
\(4,\\ a,\dfrac{x+5}{x+1}=1+\dfrac{4}{x+1}\in Z\Leftrightarrow4⋮x+1\\ \Leftrightarrow x+1\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Leftrightarrow x\in\left\{-5;-3;-2;0;1;3\right\}\\ b,\dfrac{2x+4}{x+3}=\dfrac{2\left(x+3\right)-2}{x+3}=2-\dfrac{2}{x+3}\in Z\\ \Leftrightarrow2⋮x+3\Leftrightarrow x+3\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow x\in\left\{-5;-4;-2;-1\right\}\)
\(5,\\ -\left|3x+\dfrac{1}{5}\right|\le0\\ \Leftrightarrow A=2017-\left|3x+\dfrac{1}{5}\right|\le2017\\ A_{max}=2017\Leftrightarrow3x+\dfrac{1}{5}=0\Leftrightarrow x=-\dfrac{1}{15}\\ 6,\\ \left\{{}\begin{matrix}\left(x+\dfrac{1}{2}\right)^2\ge0\\\left|2y-\dfrac{3}{4}\right|\ge0\end{matrix}\right.\Leftrightarrow A=\left(x+\dfrac{1}{2}\right)^2+\left|2y-\dfrac{3}{4}\right|+\dfrac{175}{3}\ge\dfrac{175}{3}\\ A_{min}=\dfrac{175}{3}\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{2}=0\\2y-\dfrac{3}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{3}{8}\end{matrix}\right.\)
Bài 5:
\(A=-\left|3x+\dfrac{1}{5}\right|+2017\le2017\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{1}{15}\)

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40
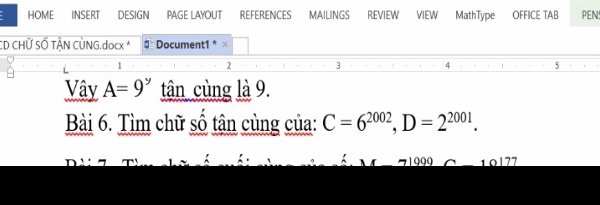


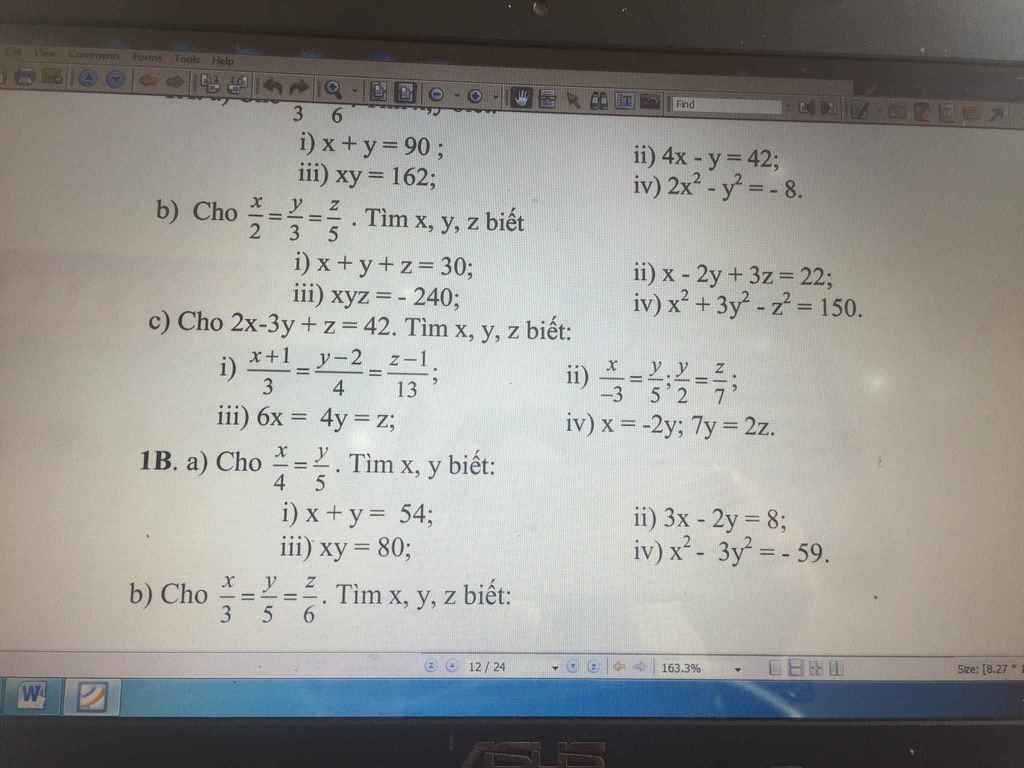

 Mọi người giúp mik câu h,i bài 2; bài 3 với
Mọi người giúp mik câu h,i bài 2; bài 3 với




\(C=6^{2002}=\overline{...6}\)( các số tận cùng là 6 nhân với nhau tận cùng cũng là 6 )
\(D=2^{2001}=\left(2^4\right)^{500}.2=\overline{...6}.2=\overline{...2}\) ( vì 2 mũ 4 có tận cùng là 6 )