Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 10:
a: \(3^{35}=2187^5\)
\(5^{20}=625^5\)
mà 2187>625
nên \(3^{35}>5^{20}\)
b: \(2^{32}=16^8< 37^8\)

Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40


Đây là toán nâng cao chuyên đề tìm phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp đánh giá như sau:
Giải:
20\(^x\) : 14\(^x\) = \(\dfrac{10}{7}\)\(x\) (\(x\) \(\in\) N)
\(\left(\dfrac{20}{14}\right)^x\) = \(\dfrac{10}{7}\)⇒ \(x\)\(\left(\dfrac{10}{7}\right)^x\) = \(\dfrac{10}{7}\)\(x\)
\(x\) = \(\left(\dfrac{10}{7}\right)^x\): \(\dfrac{10}{7}\) ⇒ \(x\) =\(\left(\dfrac{10}{7}\right)^{x-1}\)
Nếu \(x\) = 0 ta có 0 = (\(\dfrac{10}{7}\))-1 = \(\dfrac{7}{10}\) (vô lý)
Nếu \(x\) = 1 ta có: 1 = \(\left(\dfrac{10}{7}\right)^{1-1}\) = 1 (nhận)
Nếu \(x\) > 1 ta có: \(x\) \(\in\) N mà (\(\dfrac{10}{7}\))\(x\) không phải là số tự nhiên nên
\(x\) \(\ne\) (\(\dfrac{10}{7}\))\(x-1\) (loại)
Từ những lập luận trên ta có \(x\) = 1 là số tự nhiên duy nhất thỏa mãn đề bài.
Vậy \(x\) = 1

Lời giải:
$2x+xy-2y=7$
$x(2+y)-2y=7$
$x(2+y)-2(y+2)=3$
$(x-2)(y+2)=3$
Do $x,y$ là số nguyên nên $x-2, y+2$ cũng là số nguyên. Do đó ta có bảng sau:
| x-2 | 1 | 3 | -1 | -3 |
| y+2 | 3 | 1 | -3 | -1 |
| x | 3 | 5 | 1 | -1 |
| y | 1 | -1 | -5 | -3 |
| Kết luận | thỏa mãn | thỏa mãn | thỏa mãn | thỏa mãn |
\(2x+xy-2y=7\)
\(\Rightarrow x\left(2+y\right)-2y-4+4=7\)
\(\Rightarrow x\left(2+y\right)-2\left(y+2\right)=3\)
\(\Rightarrow\left(x-2\right)\left(y+2\right)=3\)
\(\Rightarrow\left(x-2\right);\left(y+2\right)\in\left\{-1;1;-3;3\right\}\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(1;-5\right);\left(3;1\right);\left(-1;-3\right);\left(5;-1\right)\right\}\left(x;y\inℤ\right)\)

 giúp đc bài nào thì giúp nhé mik đang cần gấp
giúp đc bài nào thì giúp nhé mik đang cần gấp
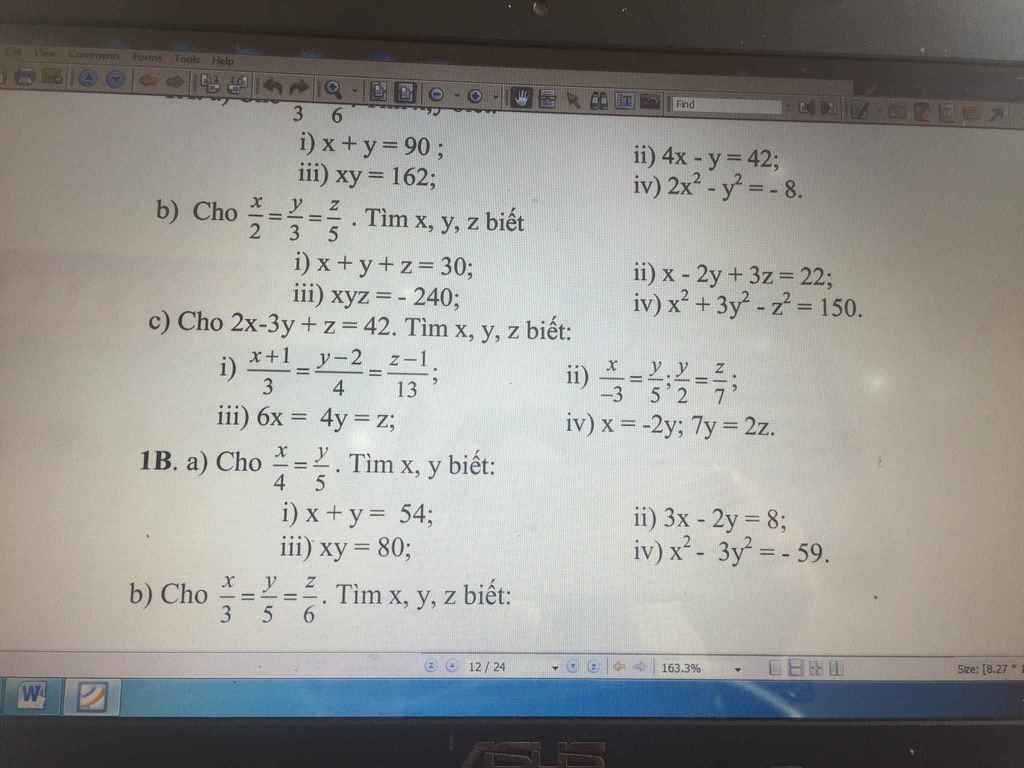
1B:
i: áp dụng tính chất của dãy tỉ só bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{x+y}{4+5}=\dfrac{54}{9}=6\)
Do đó: x=24; y=30
ii: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{3x-2y}{3\cdot4-2\cdot5}=\dfrac{8}{2}=4\)
Do đó: x=16; y=20
iii: đặt x/4=y/5=k
=>x=4k; y=5k
xy=80 nên \(20k^2=80\)
=>\(k^2=4\)
TH1: k=2
=>x=8; y=10
TH2: k=-2
=>x=-8; y=-10
a thịn ái đồ lun làm toán bất biến giữa dòng box vạn biến
a rep cmt e zesi:>