K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 3 2023
1: Diện tích vườn là 30*25=750m2
Diện tích vườn còn lại là:
28,5*23,5=669,75m2
Diện tích lối đi là:
750-669,75=80,25m2
Số viên gạch dùng tới là:
80,25*10^4:50^2=321 viên
Số tiền dùng tới là:
321*14000=4494000 đồng
25 tháng 3 2023
1: Diện tích vườn là 30*25=750m2
Diện tích vườn còn lại là:
28,5*23,5=669,75m2
Diện tích lối đi là:
750-669,75=80,25m2
Số viên gạch dùng tới là:
80,25*10^4:50^2=321 viên
Số tiền dùng tới là:
321*14000=4494000 đồng
15 tháng 12 2023
k: \(\left(4x-16\right)\left(-72+9x\right)=0\)
=>\(4\cdot\left(x-4\right)\cdot9\left(x-8\right)=0\)
=>\(36\left(x-4\right)\left(x-8\right)=0\)
=>\(\left(x-4\right)\left(x-8\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=8\end{matrix}\right.\)
m: \(\left(20+5x\right)\left(4x-8\right)=0\)
=>\(5\cdot\left(x+4\right)\cdot4\left(x-2\right)=0\)
=>\(\left(x+4\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
n: \(\left(-4x+48\right)\left(2x-24\right)=0\)
=>\(-4\left(x-12\right)\cdot2\left(x-12\right)=0\)
=>\(\left(x-12\right)^2=0\)
=>x-12=0
=>x=12
o: \(\left(4x+16\right)\left(-2x+20\right)\left(-40+x\right)=0\)
=>\(4\cdot\left(x+4\right)\cdot\left(-2\right)\left(x-10\right)\left(x-40\right)=0\)
=>\(\left(x+4\right)\left(x-10\right)\left(x-40\right)=0\)
=>\(\left[{}\begin{matrix}x+4=0\\x-10=0\\x-40=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=10\\x=40\end{matrix}\right.\)
p: \(\left(-5x+40\right)\left(-x+2023\right)\left(2x-2\right)=0\)
=>\(-5\left(x-8\right)\cdot\left(-1\right)\cdot\left(x-2023\right)\cdot2\left(x-1\right)=0\)
=>\(\left(x-8\right)\left(x-2023\right)\left(x-1\right)=0\)
=>\(\left[{}\begin{matrix}x-8=0\\x-1=0\\x-2023=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=1\\x=2023\end{matrix}\right.\)
q: \(2024x\left(4x-8\right)\left(5+5x\right)=0\)
=>\(x\cdot4\left(x-2\right)\cdot5\left(x+1\right)=0\)
=>\(x\left(x-2\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-1\end{matrix}\right.\)
r: \(-4x\left(3x+9\right)\left(2x-16\right)=0\)
=>\(-4x\cdot3\left(x+3\right)\cdot2\left(x-8\right)=0\)
=>\(x\left(x+3\right)\left(x-8\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x+3=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=8\end{matrix}\right.\)
s: \(\left(-100+5x\right)\left(2x-10\right)\left(6x+6\right)=0\)
=>\(5\cdot\left(x-20\right)\cdot2\left(x-5\right)\cdot6\left(x+1\right)=0\)
=>\(\left(x-20\right)\left(x-5\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x-20=0\\x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=20\\x=5\\x=-1\end{matrix}\right.\)
t: \(\left(-2x+4\right)\left(2x+16\right)\cdot\left(7-x\right)=0\)
=>\(-2\left(x-2\right)\cdot2\left(x+8\right)\cdot\left(-1\right)\cdot\left(x-7\right)=0\)
=>\(\left(x-2\right)\left(x+8\right)\left(x-7\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x-7=0\\x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-8\\x=7\end{matrix}\right.\)
21 tháng 1
s: \(\dfrac{-21}{46}\cdot\left(-13\right)+\dfrac{3^2}{-9}-\dfrac{-1}{2}\cdot\left(-10\right)\)
\(=\dfrac{21}{46}\cdot13-1-\dfrac{1}{2}\cdot10\)
\(=\dfrac{273}{46}-1-5=\dfrac{273}{46}-5=\dfrac{43}{46}\)
t: \(T=\left(-\dfrac{1}{7}\right)+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2024}\)
=>\(\left(-\dfrac{1}{7}\right)\cdot T=\left(-\dfrac{1}{7}\right)^2+\left(-\dfrac{1}{7}\right)^3+...+\left(-\dfrac{1}{7}\right)^{2025}\)
=>\(\left(-\dfrac{1}{7}\right)\cdot T-T=\left(-\dfrac{1}{7}\right)^2+\left(-\dfrac{1}{7}\right)^3+...+\left(-\dfrac{1}{7}\right)^{2025}-\left(-\dfrac{1}{7}\right)-\left(-\dfrac{1}{7}\right)^2-...-\left(-\dfrac{1}{7}\right)^{2024}\)
=>\(-\dfrac{8}{7}T=\left(-\dfrac{1}{7}\right)^{2025}+\dfrac{1}{7}\)
=>\(-\dfrac{8}{7}\cdot T=-\dfrac{1}{7^{2025}}+\dfrac{1}{7}\)
=>\(-\dfrac{8}{7}\cdot T=\dfrac{-1+7^{2024}}{7^{2025}}\)
=>\(T\cdot\dfrac{8}{7}=\dfrac{-7^{2024}+1}{7^{2025}}\)
=>\(T=\dfrac{-7^{2024}+1}{7^{2025}}:\dfrac{8}{7}=\dfrac{-7^{2024}+1}{7^{2024}}\cdot8\)
u: \(U=\dfrac{1}{5}-\dfrac{1}{5^2}+\dfrac{1}{5^3}-...-\dfrac{1}{5^{2024}}\)
=>\(5\cdot U=1-\dfrac{1}{5}+\dfrac{1}{5^2}-...-\dfrac{1}{5^{2023}}\)
=>\(5U+U=1-\dfrac{1}{5}+\dfrac{1}{5^2}-...-\dfrac{1}{5^{2023}}+\dfrac{1}{5}-\dfrac{1}{5^2}+...-\dfrac{1}{5^{2024}}\)
=>\(6U=1-\dfrac{1}{5^{2024}}=\dfrac{5^{2024}-1}{5^{2024}}\)
=>\(U=\dfrac{5^{2024}-1}{5^{2024}\cdot6}\)
HT
1
10 tháng 5 2016
Di chuyển con trỏ chuột đến phía trước chữ nào muốn đánh dấu sau đó nhấn và giữ nút trái chuột rồi kéo từ phải sang trái để chọn hết các chữ muốn đánh dấu.
Chúc bạn học tốt
L2
1
9 tháng 2 2020
3n2+5/n-1=6n+5/n-1=6(n-1)+11/n-1=6(n-1)/n-1+11/n-1=6+11/n-1
để n nguyên thì 6+11/n-1 nguyên mà 6+11/n-1 nguyên khi n-1 thuộc ước 11
mà ước 11 thuộc (-1;1;11;-11)
ta có bảng;.............................
AH
Akai Haruma
Giáo viên
5 tháng 8 2021
Lời giải:
Ta thấy:
$\frac{1}{2^2}< \frac{1}{1.2}$
$\frac{1}{3^2}< \frac{1}{2.3}$
$\frac{1}{4^2}< \frac{1}{3.4}$
$........$
$\frac{1}{20^2}< \frac{1}{19.20}$
Cộng lại:
$M< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{19.20}$
$M< \frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+....+\frac{20-19}{19.20}$
$M< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{19}-\frac{1}{20}$
$M< 1-\frac{1}{20}< 1$
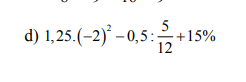
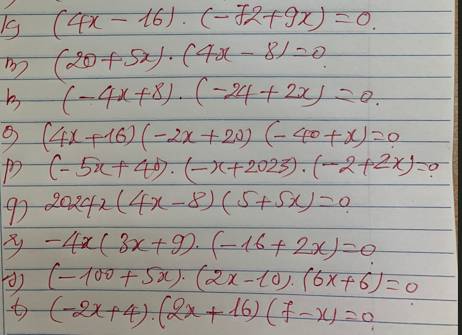
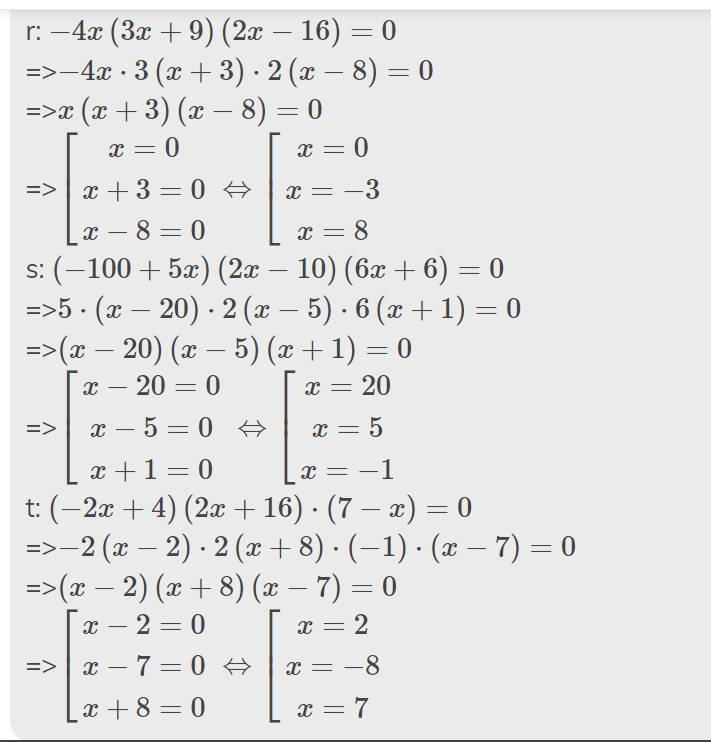
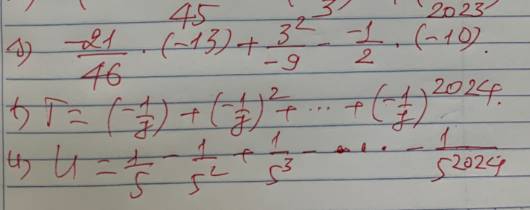
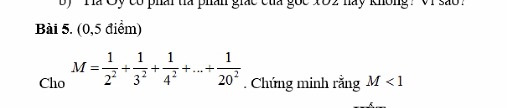
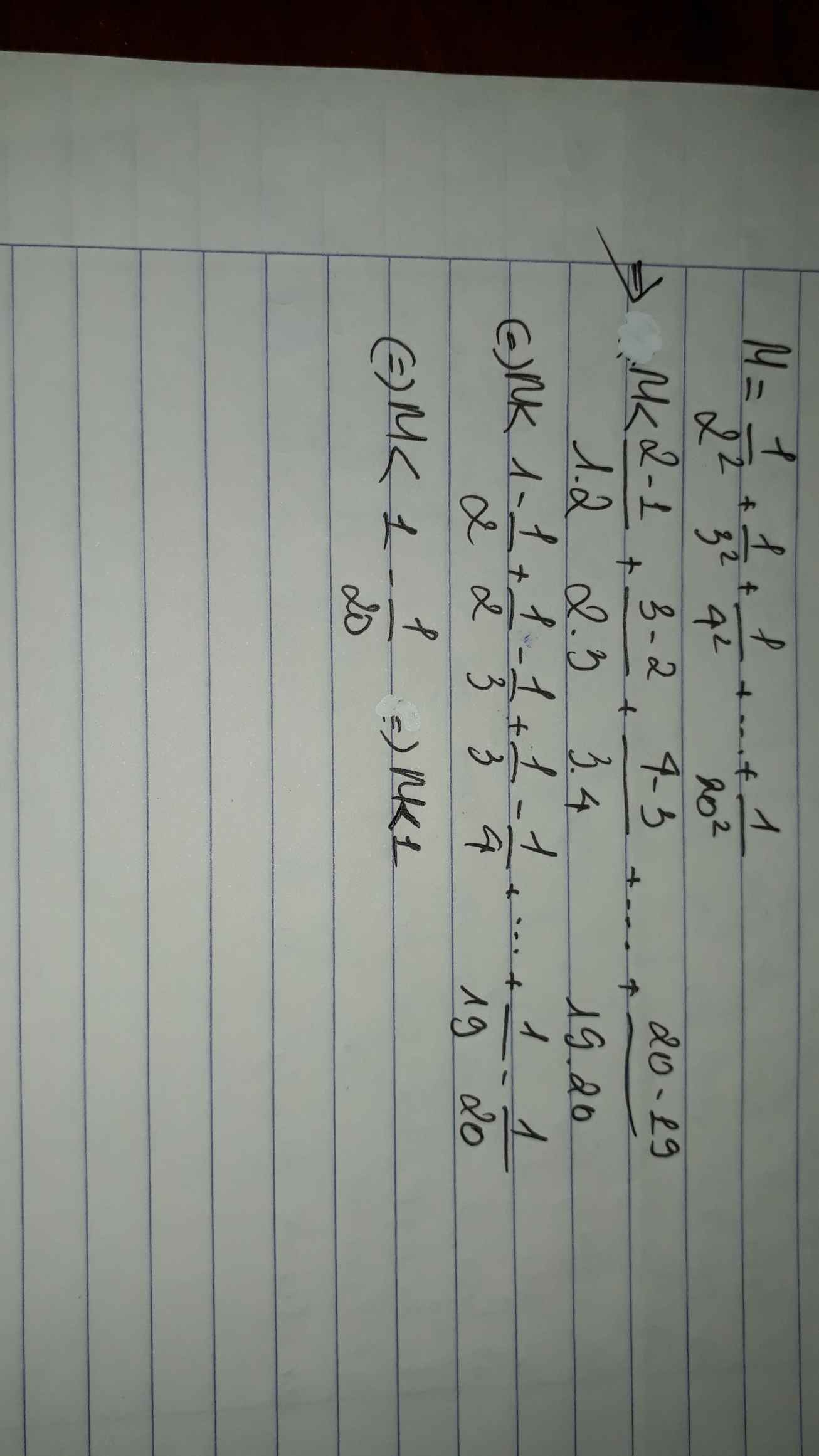
d) Ta có: \(1,25\cdot\left(-2\right)^2-0.5:\dfrac{5}{12}+15\%\)
\(=\dfrac{5}{4}\cdot4-\dfrac{1}{2}\cdot\dfrac{12}{5}+\dfrac{3}{20}\)
\(=5-\dfrac{6}{5}+\dfrac{3}{20}\)
\(=\dfrac{100}{20}-\dfrac{120}{20}+\dfrac{3}{20}\)
\(=\dfrac{-17}{20}\)