
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.

a: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{ABC}=\widehat{ECN}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BD=CE
\(\widehat{MBD}=\widehat{NCE}\)
Do đó: ΔMBD=ΔNCE
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=EN
\(\widehat{MDI}=\widehat{ENC}\)(hai góc so le trong, DM//EN)
Do đó: ΔIDM=ΔIEN
=>IM=IN
=>I là trung điểm của MN

a: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
b: Xét ΔABE và ΔACD có
AB=AC
góc A chung
AE=AD
=>ΔABE=ΔACD
c: Xét ΔIDB và ΔIEC có
góc IDB=góc IEC
DB=EC
góc IBD=góc ICE
=>ΔIDB=ΔIEC
d: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
=>góc BAI=góc CAI
=>AI là phângíac của góc BAC
e: AB=AC
IB=IC
=>AI là trung trực của BC
=>AI vuông góc BC


a)\(\Leftrightarrow\left|x+1,5\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1,5=4\\x+1,5=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2,5\\x=-5,5\end{matrix}\right.\)
c)\(\Leftrightarrow-14+21x=5+10x\)
\(\Leftrightarrow11x=19\Leftrightarrow x=\dfrac{19}{11}\)


Bài 1:
a, Xét ΔABC và ΔCDA có:
AB=CD(gt)
AD=BC(gt)
Chung AC
⇒ΔABC = ΔCDA (c.c.c)
b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)
Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC
Bn vẽ hình bài 1 cho mik đc ko ạ! Mik chưa hiểu rõ lắm!

4:
0,(3)=1/3
3,2(4)=146/45
-0,6(81)=-15/22
5:
a: 0,6(81)=0,68181...
0,68100...<0,68181...
=>0,681<0,6(81)
b: 0,(31)=0,3131...
0,3(13)=0,313131...
=>0,(31)=0,3(13)
3:
a: 5/8=0,625
-9/40=-0,225
13/100=0,13
-29/500=-0,058
b: 2/3=0,(6)
3/7=0,(428571)
-5/6=-0,8(3)
-4/11=-0,(36)

x và y tỉ lệ thuận
nên \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{2x_1-3x_2}{2y_1-3y_2}=\dfrac{42.5}{-8.5}=-5\)
=>x=-5y




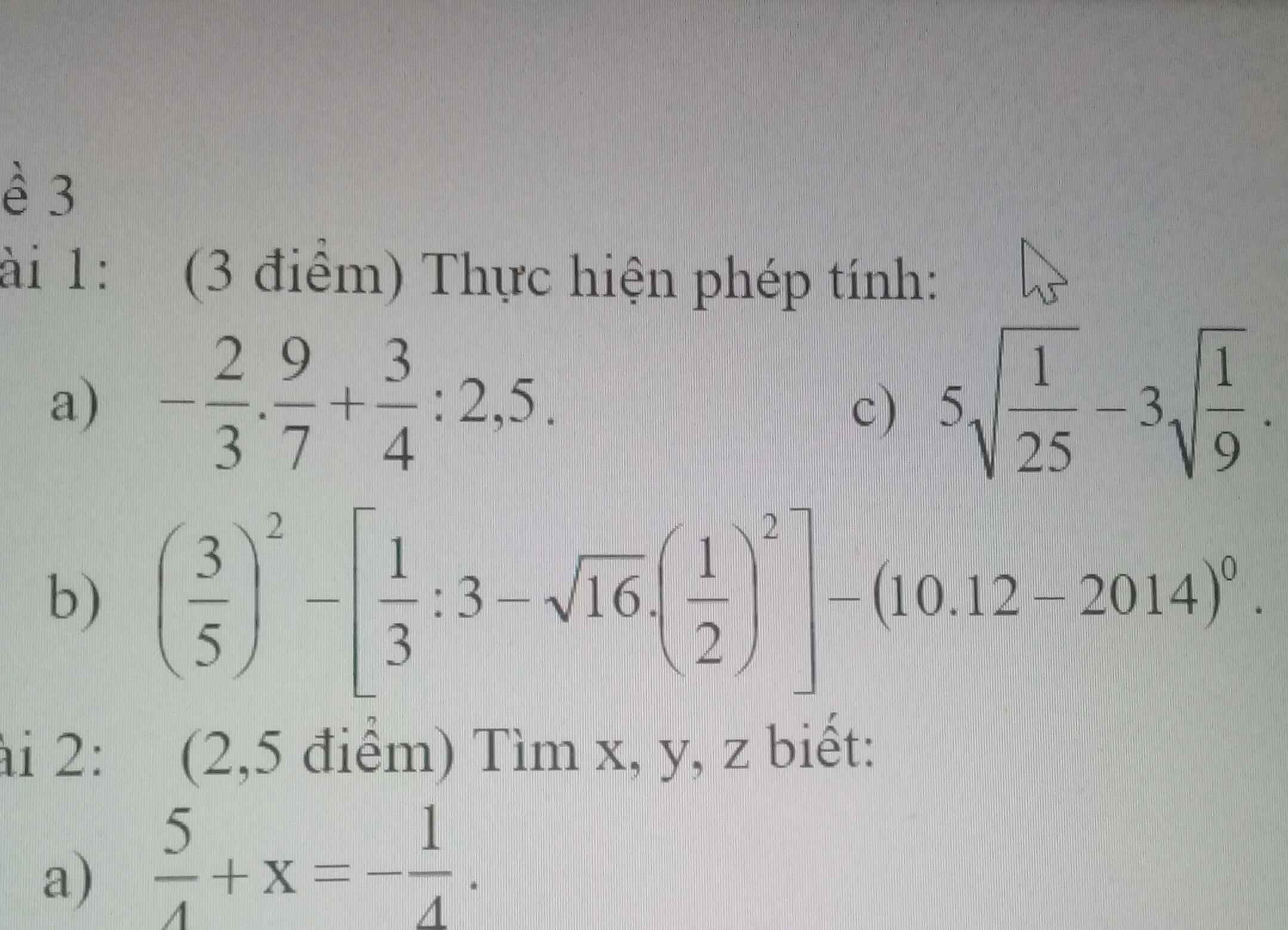
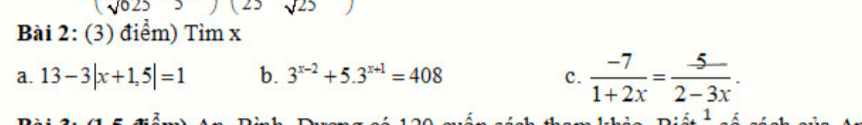

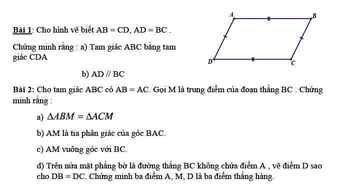
 giúp em vs ak em câaần gấsp ạ
giúp em vs ak em câaần gấsp ạ