
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mik cần lời giải á, các bạn toàn cho mik đáp án hoặc là cho mỗi câu 123 (Q▪︎Q)

Bài 3:
a) Ta có: \(\left(x+10\right)^2+\left(x-10\right)^2\)
\(=x^2+20x+100+x^2-20x+100\)
\(=2x^2+200\)
b) Ta có: \(\left(x-12\right)^2+\left(x+12\right)^2\)
\(=x^2-24x+144+x^2+24x+144\)
\(=2x^2+288\)
c) Ta có: \(\left(x+7\right)^2-\left(x-7\right)^2\)
\(=\left(x+7-x+7\right)\left(x+7+x-7\right)\)
\(=14\cdot2x\)
=28x
Bài 1:
a) Ta có: \(\left(a+12\right)^2\)
\(=a^2+2\cdot a\cdot12+12^2\)
\(=a^2+24a+144\)
b) Ta có: \(\left(3a+\dfrac{1}{3}\right)^2\)
\(=\left(3a\right)^2+2\cdot3a\cdot\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2\)
\(=9a^2+2a+\dfrac{1}{9}\)
c) Ta có: \(\left(5a^2+6\right)^2\)
\(=\left(5a^2\right)^2+2\cdot5a^2\cdot6+6^2\)
\(=25a^4+60a^2+36\)
d) Ta có: \(\left(\dfrac{1}{2}+4b\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2+2\cdot\dfrac{1}{2}\cdot4b+\left(4b\right)^2\)
\(=\dfrac{1}{4}+4b+16b^2\)
e) Ta có: \(\left(a^m+b^n\right)^2\)
\(=\left(a^m\right)^2+2\cdot a^m\cdot b^n+\left(b^n\right)^2\)
\(=a^{2m}+2a^mb^n+b^{2n}\)


\(3,\)
Vì đa thức có nghiệm là \(\dfrac{1}{2}\) nên \(P\left(\dfrac{1}{2}\right)=\dfrac{1}{4}a+\dfrac{5}{2}-3=0\)
\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{1}{2}\Leftrightarrow a=2\)
\(4,\)
\(a,P\left(x\right)=3-2x=0\Leftrightarrow x=\dfrac{3}{2}\)
\(b,Q\left(x\right)=x^2+2\ge2>0\)
Vậy \(Q\left(x\right)\) luôn dương hay \(Q\left(x\right)\) vô nghiệm

Bài 1.
a. $=a^2+2.a.12+12^2=a^2+24a+144$
b. $=(3a)^2+2.3a.\frac{1}{3}+(\frac{1}{3})^2=9a^2+2a+\frac{1}{9}$
c. $=(5a^2)^2+2.5a^2.6+6^2=25a^4+60a^2+36$
d. $=\frac{1}{4}+2.\frac{1}{2}.4b+(4b)^2$
$=\frac{1}{4}+4b+16b^2$
e.
$=(a^m)^2+2.a^m.b^n+(b^n)^2$
$=a^{2m}+2a^mb^n+b^{2n}$
Bài 2.
$(x-0,3)^2=x^2-0,6x+0,09$
$(6x-3y)^2=36x^2-36xy+9y^2$
$(5-2xy)^2=25-20xy+4x^2y^2$
$(x^4-1)^2=x^8-2x^4+1$
$(x^5-y^3)^2=x^{10}-2x^5y^3+y^6$

a: \(AO=\dfrac{1}{2}AC\)(O là trung điểm của AC)
nên AO=AD
hay ΔAOD cân tại A

Bài 1:
a) \(\left(2x+y\right)^2-\left(y-2x\right)^2=\left(2x+y-y+2x\right)\left(2x+y+y-2x\right)=8xy\)
b) \(\left(x-y\right)^2+2\left(x^2-y^2\right)+\left(x+y\right)^2\\ =x^2-2xy+y^2+2x^2-2y^2+x^2+2xy+y^2\\ =4x^2\)
c) \(\left(x-2y\right)\left(x+2y\right)=x^2-4y^2\)
d) \(\left(y-\dfrac{1}{2}\right)\left(y+\dfrac{1}{2}\right)=y^2-\dfrac{1}{4}\)
Bài 1:
a: \(\left(2x+y\right)^2-\left(y-2x\right)^2\)
\(=4x^2+4xy+y^2-y^2+4xy-4x^2\)
=8xy
b: Ta có: \(\left(x-y\right)^2+2\left(x^2-y^2\right)+\left(x+y\right)^2\)
\(=\left(x-y+x+y\right)^2\)
\(=\left(2x\right)^2\)
\(=4x^2\)
c: \(\left(x-2y\right)\left(x+2y\right)=x^2-4y^2\)
d: \(\left(y-\dfrac{1}{2}\right)\left(y+\dfrac{1}{2}\right)=y^2-\dfrac{1}{4}\)

Bài 2:
Gọi K là trung điểm của AD và O là trung điểm của BC
Xét ΔABC có
P là trung điểm của AC
O là trung điểm của BC
Do đó: PO là đường trung bình của ΔABC
Suy ra: PO//AB
hay PO//CD
Xét ΔDAB có
K là trung điểm của AD
Q là trung điểm của BD
Do đó: KQ là đường trung bình của ΔDAB
Suy ra: KQ//AB
hay KQ//CD
Xét ΔBDC có
Q là trung điểm của BD
O là trung điểm của BC
Do đó: QO là đường trung bình của ΔBDC
Suy ra: QO//DC
Ta có: QO//DC
mà PO//DC
và QO,PO có điểm chung là O
nên Q,P,O thẳng hàng
Ta có: KQ//CD
QO//CD
mà KQ và QO có điểm chung là Q
nên K,Q,O thẳng hàng
mà Q,P,O thẳng hàng
nên K,Q,P,O thẳng hàng
hay QP//DC(1)
Xét ΔEAB có
M là trung điểm của EA
N là trung điểm của EB
Do đó: MN là đường trung bình của ΔEAB
Suy ra: MN//AB
hay MN//DC(2)
Từ (1) và (2) suy ra MN//PQ
Xét tứ giác MNPQ có MN//PQ
nên MNPQ là hình thang




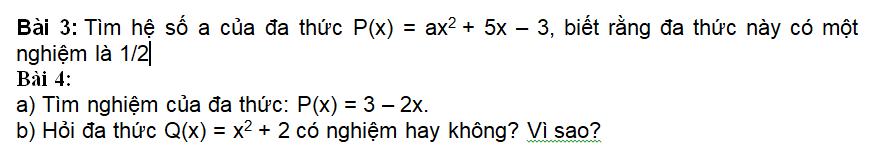

 Giúp em với, em đg cần thực sự gấp ạ!!!
Giúp em với, em đg cần thực sự gấp ạ!!!
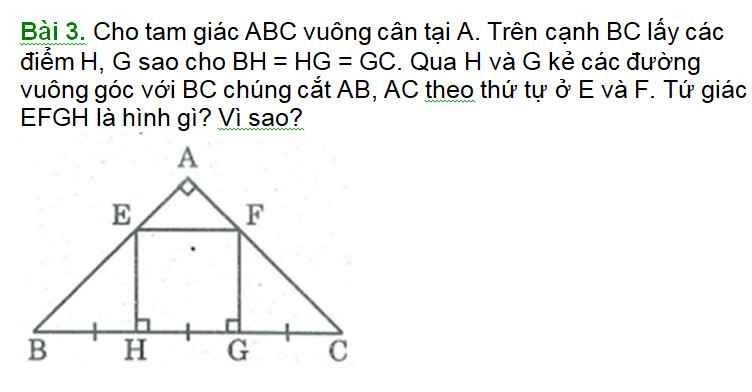
Xét tứ giác EHGF có:
EH//GF(cùng vuôn góc BC)
\(\widehat{EHG}=90^0\)(EH⊥HG)
=> EHGF là hình chữ nhật(1)
Xét tam giác EBG có:
EH là đường cao(EH⊥BG)
EH là trung tuyến(BH=HG)
=> Tam giác EBG cân tại E
Mà \(\widehat{EBH}=45^0\)(ABC vuông cân tại A)
=> Tam giác EBG vuông cân tại E
=> \(EH=\dfrac{1}{2}BG=HG\left(2\right)\)(EH là trung tuyến ứng với cạnh huyền)
\(\left(1\right),\left(2\right)\Rightarrow\) EHGF là hình vuông
Em cảm ơn ạ