
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a) Ta có: \(\left(x+10\right)^2+\left(x-10\right)^2\)
\(=x^2+20x+100+x^2-20x+100\)
\(=2x^2+200\)
b) Ta có: \(\left(x-12\right)^2+\left(x+12\right)^2\)
\(=x^2-24x+144+x^2+24x+144\)
\(=2x^2+288\)
c) Ta có: \(\left(x+7\right)^2-\left(x-7\right)^2\)
\(=\left(x+7-x+7\right)\left(x+7+x-7\right)\)
\(=14\cdot2x\)
=28x
Bài 1:
a) Ta có: \(\left(a+12\right)^2\)
\(=a^2+2\cdot a\cdot12+12^2\)
\(=a^2+24a+144\)
b) Ta có: \(\left(3a+\dfrac{1}{3}\right)^2\)
\(=\left(3a\right)^2+2\cdot3a\cdot\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2\)
\(=9a^2+2a+\dfrac{1}{9}\)
c) Ta có: \(\left(5a^2+6\right)^2\)
\(=\left(5a^2\right)^2+2\cdot5a^2\cdot6+6^2\)
\(=25a^4+60a^2+36\)
d) Ta có: \(\left(\dfrac{1}{2}+4b\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2+2\cdot\dfrac{1}{2}\cdot4b+\left(4b\right)^2\)
\(=\dfrac{1}{4}+4b+16b^2\)
e) Ta có: \(\left(a^m+b^n\right)^2\)
\(=\left(a^m\right)^2+2\cdot a^m\cdot b^n+\left(b^n\right)^2\)
\(=a^{2m}+2a^mb^n+b^{2n}\)


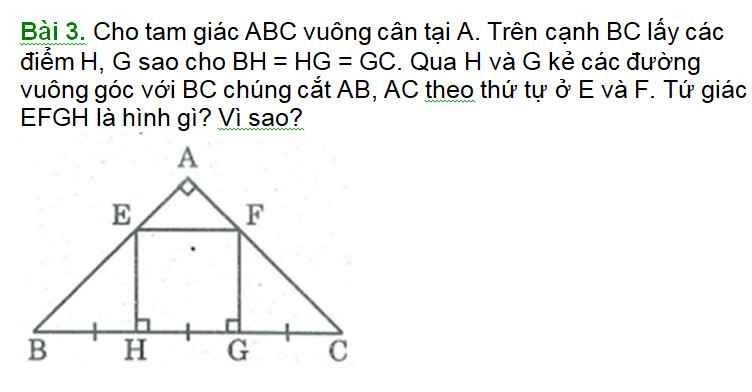
Xét tứ giác EHGF có:
EH//GF(cùng vuôn góc BC)
\(\widehat{EHG}=90^0\)(EH⊥HG)
=> EHGF là hình chữ nhật(1)
Xét tam giác EBG có:
EH là đường cao(EH⊥BG)
EH là trung tuyến(BH=HG)
=> Tam giác EBG cân tại E
Mà \(\widehat{EBH}=45^0\)(ABC vuông cân tại A)
=> Tam giác EBG vuông cân tại E
=> \(EH=\dfrac{1}{2}BG=HG\left(2\right)\)(EH là trung tuyến ứng với cạnh huyền)
\(\left(1\right),\left(2\right)\Rightarrow\) EHGF là hình vuông

\(5x\left(3x^2y-2xy^2+1\right)-3xy\left(5x^2-3xy\right)+x^2y^2-10=0\)
\(\Leftrightarrow15x^3y-10x^2y^2+5x-15x^3y+9x^2y^2+x^2y^2-10=0\)
\(\Leftrightarrow5x-10=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)

\(x^2+\left(x+3\right)\left(x-9\right)=-27\\ \Rightarrow x^2+x^2+3x-9x-27=-27\\ \Rightarrow2x^2-6x=0\\ \Rightarrow2x\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
\(x^2+\left(x+3\right)\left(x-9\right)=-27\)
\(\Rightarrow2x^2-6x=0\)
\(\Rightarrow2x\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)

c: Ta có: \(\left(x-3\right)^3-\left(x^3-27\right)+9\left(x+1\right)^2=15\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+9\left(x^2+2x+1\right)=15\)
\(\Leftrightarrow-9x^2+27x+9x^2+18x+9=15\)
\(\Leftrightarrow45x=6\)
hay \(x=\dfrac{2}{15}\)
d: Ta có: \(x\left(x-5\right)\left(x+5\right)-\left(x^3+8\right)=3\)
\(\Leftrightarrow x^3-25x-x^3-8=3\)
\(\Leftrightarrow-25x=11\)
hay \(x=-\dfrac{11}{25}\)

Bài 1.
a. $=a^2+2.a.12+12^2=a^2+24a+144$
b. $=(3a)^2+2.3a.\frac{1}{3}+(\frac{1}{3})^2=9a^2+2a+\frac{1}{9}$
c. $=(5a^2)^2+2.5a^2.6+6^2=25a^4+60a^2+36$
d. $=\frac{1}{4}+2.\frac{1}{2}.4b+(4b)^2$
$=\frac{1}{4}+4b+16b^2$
e.
$=(a^m)^2+2.a^m.b^n+(b^n)^2$
$=a^{2m}+2a^mb^n+b^{2n}$
Bài 2.
$(x-0,3)^2=x^2-0,6x+0,09$
$(6x-3y)^2=36x^2-36xy+9y^2$
$(5-2xy)^2=25-20xy+4x^2y^2$
$(x^4-1)^2=x^8-2x^4+1$
$(x^5-y^3)^2=x^{10}-2x^5y^3+y^6$
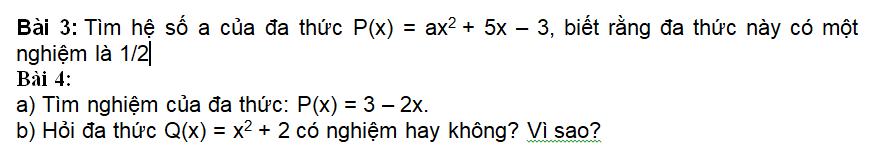


 giúp e với e đg cần rất rất gấp ạ
giúp e với e đg cần rất rất gấp ạ
\(3,\)
Vì đa thức có nghiệm là \(\dfrac{1}{2}\) nên \(P\left(\dfrac{1}{2}\right)=\dfrac{1}{4}a+\dfrac{5}{2}-3=0\)
\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{1}{2}\Leftrightarrow a=2\)
\(4,\)
\(a,P\left(x\right)=3-2x=0\Leftrightarrow x=\dfrac{3}{2}\)
\(b,Q\left(x\right)=x^2+2\ge2>0\)
Vậy \(Q\left(x\right)\) luôn dương hay \(Q\left(x\right)\) vô nghiệm
E cảm ơn ạ