K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LK
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
1
28 tháng 10 2023
6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em với ạ em cần gấp ạ
31 tháng 8 2023
1: \(\sqrt{11}\) là số vô tỉ
2:
a: 4,9(18)=4,91818...
mà 4,91818<4,928
nên 4,9(18)<4,928
b: 4,315<4,318
=>-4,315>-4,318
=>-4,315...>-4,318...
c: \(\sqrt{3}=\sqrt{\dfrac{6}{2}}< \sqrt{\dfrac{7}{2}}\)
3:
a: \(6=\sqrt{3};-1,7=-\sqrt{2,89}\)
0<2,89<3
=>\(0< \sqrt{2,89}< \sqrt{3}\)
=>\(-\sqrt{3}< -\sqrt{2,89}< 0\)
0<35<36<47
=>\(0< \sqrt{35}< \sqrt{36}< \sqrt{47}\)
=>\(-\sqrt{3}< -\sqrt{2,89}< 0< \sqrt{35}< \sqrt{36}< \sqrt{47}\)
=>\(-\sqrt{3}< -\sqrt{2,89}< 0< \sqrt{35}< 6< \sqrt{47}\)
b: \(-\sqrt{2\dfrac{1}{3}}=-\sqrt{2,\left(3\right)}\)
\(-1,5=-\sqrt{2,25}\)
2,25<2,3<2,(3)
=>\(\sqrt{2.25}< \sqrt{2.3}< \sqrt{2.\left(3\right)}\)
=>\(0>-1.5>-\sqrt{2.3}>-\sqrt{2\dfrac{1}{3}}\)
\(0< \sqrt{5\dfrac{1}{6}}=\sqrt{5,1\left(6\right)}< \sqrt{5,3}\)
=>\(\sqrt{5.3}>\sqrt{5\dfrac{1}{6}}>0>-1.5>-\sqrt{2.3}>-\sqrt{2\dfrac{1}{3}}\)
giúp em với ạ em cần gấp ạ
H9
HT.Phong (9A5)
CTVHS
3 tháng 9 2023
a) Ta có:
\(\widehat{yOu}+\widehat{xOy}=180^o\) (kề bù)
\(\Rightarrow\widehat{yOu}=180^o-\widehat{xOy}\)
\(\Rightarrow\widehat{yOu}=180^o-60^o=120^o\)
Mà: \(\widehat{xOt}+\widehat{tOu}=180^o\) (kề bù)
\(\Rightarrow\widehat{xOt}=180^o-\widehat{tOu}\)
\(\Rightarrow\widehat{xOt}=180^o-30^o=150^o\)
b) Ta có:
\(\widehat{xOy}+\widehat{yOt}+\widehat{tOu}=\widehat{xOu}\)
\(\Rightarrow\widehat{yOt}=\widehat{xOu}-\widehat{xOy}-\widehat{tOu}\)
\(\Rightarrow\widehat{yOt}=180^o-60^o-30^o\)
\(\Rightarrow\widehat{yOt}=90^o\)
3 tháng 1
`#1231.2021`
`1.`
Ta có:
`y` tỉ lệ nghịch với `x` theo hệ số tỉ lệ `-4`
`=> y = (-4)/x` `(1)`
`x` tỉ lệ nghịch với `z` theo hệ số tỉ lệ `3/4`
`=> x = 3/4 \div z` `(2)`
Thay `(2)` vào `(1)`
`=> y = (-4)/(3/4 \div z) => y = -16/3 * z`
Vậy, `y` và `z` tỉ lệ thuận với nhau theo hệ số tỉ lệ `-16/3`
`=> A.`
giúp em với ạ nhanh em cần ạ :33
giúp em với ạ em đang cần gấp ạ
3 tháng 7 2023
Bài 16
a) \(A=\dfrac{n+1}{n+2}\)
Gọi ƯCLN(n+1;n+2) là x ( \(x\in N\) *)
\(\Rightarrow\) \(\left\{{}\begin{matrix}\left(n+1\right)⋮x\\\left(n+2\right)⋮x\end{matrix}\right.\)
\(\Rightarrow\) \(\left(n+2\right)-\left(n+1\right)\) \(⋮x\)
\(\Rightarrow\) \(1\) \(⋮x\)
\(\Rightarrow\) x = 1 \(\Rightarrow\) ƯCLN(n+1;n+2)=1
Vậy A là phân số tối giản ( vì có ƯCLN = 1)
b) \(B=\dfrac{n+1}{3n+4}\)
Gọi ƯCLN(n+1;3n+4) là d ( \(d\in N\) *)
\(\Rightarrow\) \(\left\{{}\begin{matrix}n+1⋮d\\3n+4⋮d\end{matrix}\right.\)
\(\Rightarrow\) \(\left\{{}\begin{matrix}3n+3⋮d\\3n+4⋮d\end{matrix}\right.\)
\(\Rightarrow\) (3n+4)-(3n+3) chia hết cho d
\(\Rightarrow\) \(1⋮d\)
\(\Rightarrow\) d =1
Vậy B là phân số tối giản.
Mấy phần kia tương tự
3 tháng 7 2023
c: Gọi d=ƯCLN(3n+2;5n+3)
=>3n+2 chia hết cho d và 5n+3 chia hết cho d
=>15n+10 chia hết cho d và 15n+9 chia hết cho d
=>1 chia hết cho d
=>ƯCLN(3n+2;5n+3)=1
=>PSTG
d: Gọi d=ƯCLN(12n+1;30n+2)
=>12n+1 và 30n+2 đều chia hết cho d
=>60n+5 chia hết cho d và 60n+4 chia hết cho d
=>1 chia hết cho d
=>d=1
=>PSTG
giúp em với ạ em đang cần gấp ạ :(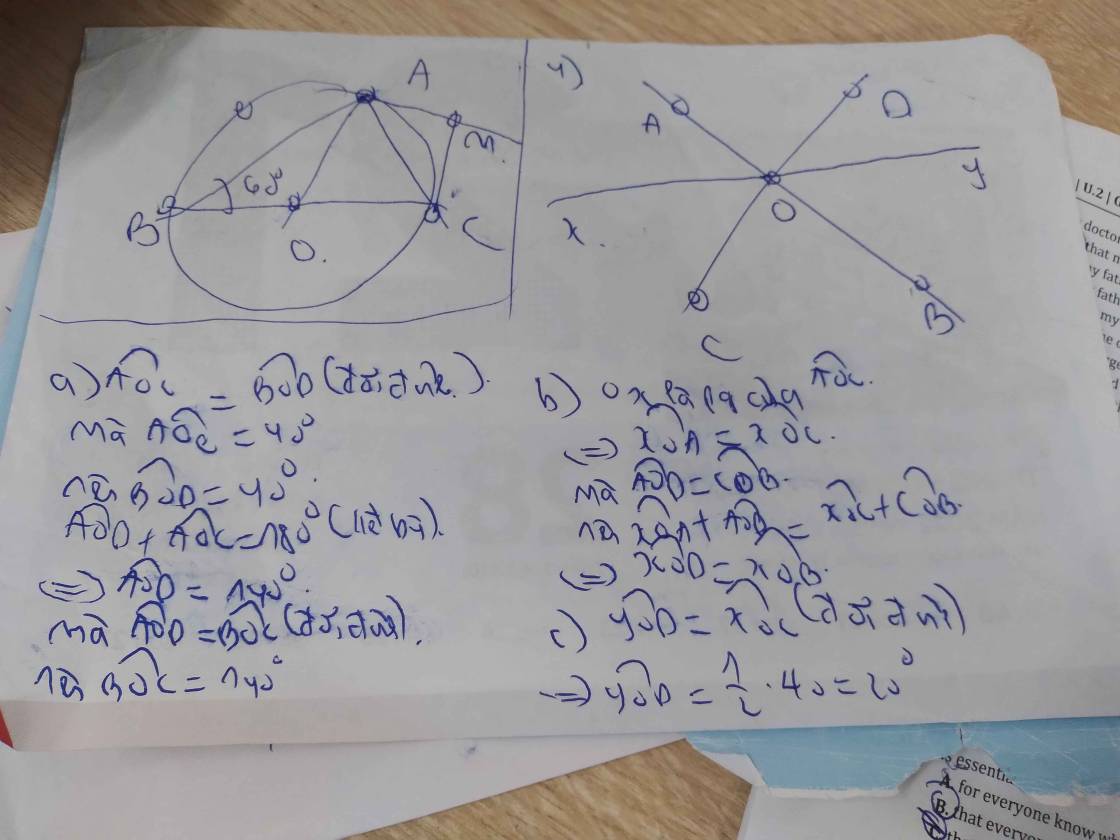
`Answer:`
\(A=\frac{1}{2}x^2y^3-4xy+5\)
Thay `x=-2` và `y=2/3` vào đa thức `A`, ta được:
\(A=\frac{1}{2}.\left(-2\right)^2.\frac{2}{3}^3-4.\left(-2\right).\frac{2}{3}+5\)
\(=\frac{1}{2}.4.\frac{8}{27}-4.-2.\frac{2}{3}+5\)
\(=\frac{16}{27}-\frac{-16}{3}+5\)
\(=\frac{295}{27}\)