
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(B=\dfrac{2x+3\sqrt{x}+9}{x-9}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{2x+3\sqrt{x}+9-x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x+6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)



Câu 9:
a: \(A=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(x+1\right)}+\dfrac{1}{x+1}\right)\cdot\dfrac{x+1}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}+1}{x+1}\cdot\dfrac{x+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b: Thay \(x=4+2\sqrt{3}\) vào A, ta đc:
\(A=\dfrac{\sqrt{3}+1+1}{\sqrt{3}+1-1}=\dfrac{2+\sqrt{3}}{\sqrt{3}}\)
c: Để A nguyên thì \(\sqrt{x}-1+2⋮\sqrt{x}-1\)
=>\(\sqrt{x}-1\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{4;0;9\right\}\)

Lời giải:
a. Áp dụng hệ thức lượng trong tam giác vuông ta có:
$AH^2=BH.CH=4.6=24$
$\Rightarrow AH=\sqrt{24}=2\sqrt{6}$ (cm)
$AB^2=BH.BC=BH(BH+CH)=4(4+6)=40$
$\Rightarrow AB=\sqrt{40}=2\sqrt{10}$ (cm)
b.
$AC^2=CH.BC=6(6+4)=60$
$\Rightarrow AC=\sqrt{60}=2\sqrt{15}$ (cm)
$AM=AC:2=\sqrt{15}$ (cm)
$\tan \widehat{AMB}=\frac{AB}{AM}=\frac{2\sqrt{10}}{\sqrt{15}}=\frac{2\sqrt{6}}{3}$
$\Rightarrow \widehat{AMB}=59^0$
c.
Áp dụng hệ thức lượng trong tam giác vuông với tam giác $ABM$:
$BK.BM=AB^2(1)$
Áp dụng hệ thức lượng với tam giác $ABC$:
$AB^2=BH.BC(2)$
Từ $(1); (2)\Rightarrow BK.BM=BH.BC$

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >25\end{matrix}\right.\)
b: \(A=\sqrt{x}+\sqrt{x}+2=2\sqrt{x}+2\)


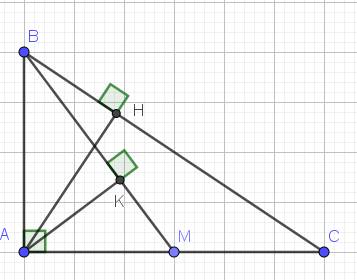
a: Xét (O) có
OH là một phần đường kính
AB là dây
OH⊥AB tại H
Do đó: H là trung điểm của AB
Xét ΔMAB có
MH là đường cao
MH là đường trung tuyến
Do đó: ΔAMB cân tại M

Hệ có nghiệm duy nhất khi \(m^2\ne1\Rightarrow m\ne\pm1\)
Khi đó: \(\left\{{}\begin{matrix}x+my=m+1\\m^2x+my=3m^2-m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+my=m+1\\\left(m^2-1\right)x=3m^2-2m-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3m+1}{m+1}\\y=\dfrac{m-1}{m+1}\end{matrix}\right.\)
Đặt \(P=xy=\dfrac{\left(3m+1\right)\left(m-1\right)}{\left(m+1\right)^2}=\dfrac{3m^2-2m-1}{\left(m+1\right)^2}=\dfrac{-\left(m+1\right)^2+4m^2}{\left(m+1\right)^2}\)
\(=-1+\left(\dfrac{2m}{m+1}\right)^2\ge-1\)
\(P_{min}=-1\) khi \(m=0\)

 Giúp em với ạ, em cảm ơn ạ
Giúp em với ạ, em cảm ơn ạ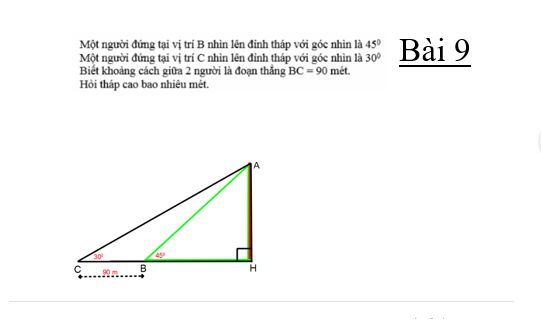 giúp em với ạ. Em cảm ơn ạ
giúp em với ạ. Em cảm ơn ạ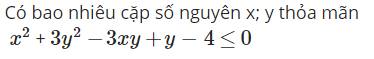





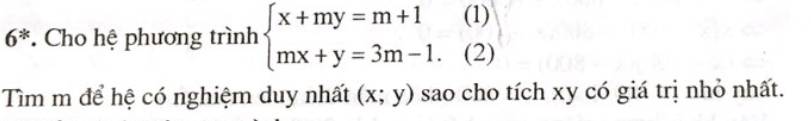
\(T=\left(\dfrac{x}{2}+\dfrac{y}{2}-\dfrac{x\sqrt{y}+y\sqrt{x}}{x+y}+\dfrac{3}{4}\right)\left(4040+\dfrac{x}{y}+\dfrac{y}{x}\right)\)
\(T\ge\left(\dfrac{x}{2}+\dfrac{y}{2}-\dfrac{x\sqrt{y}+y\sqrt{x}}{2\sqrt{xy}}+\dfrac{3}{4}\right)\left(4040+\dfrac{x}{y}+\dfrac{y}{x}\right)\)
\(T\ge\left(\dfrac{x}{2}+\dfrac{y}{2}-\dfrac{\sqrt{x}}{2}-\dfrac{\sqrt{y}}{2}+\dfrac{3}{4}\right)\left(4040+2\sqrt{\dfrac{xy}{xy}}\right)\)
\(T\ge\left[\dfrac{1}{2}\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{2}\left(\sqrt{y}-\dfrac{1}{2}\right)^2+\dfrac{1}{2}\right].4042\)
\(T\ge\dfrac{4042}{2}=2021\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{4}\)