K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
0
HN
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+61x\ge0\\4x+2\ge0\\x^2+61x\le\left(4x+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge0\\x\le-61\end{matrix}\right.\\x\ge-\dfrac{1}{2}\\15x^2-45x+4\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x\ge\dfrac{45+\sqrt{1785}}{30}\\x\le\dfrac{45-\sqrt{1785}}{30}\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}0\le x\le\dfrac{45-\sqrt{1785}}{30}\\x\ge\dfrac{45+\sqrt{1785}}{30}\end{matrix}\right.\)
2 tháng 2
5: ĐKXĐ: \(\left\{{}\begin{matrix}x^2+3x-4>=0\\2x^2-2x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+4\right)\left(x-1\right)>=0\\2x\left(x-1\right)>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=1\\x< =-4\end{matrix}\right.\\\left[{}\begin{matrix}x>=1\\x< =0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x>=1\\x< =-4\end{matrix}\right.\)
\(\sqrt{x^2+3x-4}< \sqrt{2x^2-2x}\)
=>\(x^2+3x-4< 2x^2-2x\)
=>\(2x^2-2x-x^2-3x+4>0\)
=>\(x^2-5x+4>0\)
=>(x-1)(x-4)>0
=>\(\left[{}\begin{matrix}x>4\\x< 1\end{matrix}\right.\)
Kết hợp ĐKXĐ, ta được:
\(\left[{}\begin{matrix}x>4\\x< =-4\end{matrix}\right.\)
7: ĐKXĐ: x>=-1
\(2\sqrt{x+2+2\sqrt{x+1}}-\sqrt{x+1}=4\)
=>\(2\cdot\sqrt{x+1+2\sqrt{x+1}+1}-\sqrt{x+1}=4\)
=>\(2\cdot\sqrt{\left(\sqrt{x+1}+1\right)^2}-\sqrt{x+1}=4\)
=>\(2\left(\sqrt{x+1}+1\right)-\sqrt{x+1}=4\)
=>\(\sqrt{x+1}+2=4\)
=>\(\sqrt{x+1}=2\)
=>x+1=4
=>x=3(nhận)
NH
1
30 tháng 4 2023
1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t
TT
1
25 tháng 3 2023
1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25
NH
2
6 tháng 3 2023
1: vecto AC=(-2;2)
=>VTCP là (-2;2); vtpt là (2;2)
2: vecto AB=(-10;-2)=(5;1)
=>VTPT của Δ là (5;1)
vtcp của Δ là (-1;5)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
\(\overrightarrow{AC}=\left(-2;2\right)=2\left(-1;1\right)\) nên đường thẳng AC nhận \(\left(-1;1\right)\) là 1 vtcp và \(\left(1;1\right)\) là 1 vtpt
b.
\(\overrightarrow{BA}=\left(10;2\right)=2\left(5;1\right)\) ; mà \(\Delta\perp AB\) nên \(\Delta\) nhận (5;1) là 1 vtpt và \(\left(1;-5\right)\) là 1 vtcp
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
\(B_2=\left\{x;x=2k,k\in N\right\}\)
\(B_4=\left\{x;x=4m,m\in N\right\}\)
Do \(4m=2.\left(2m\right)\Rightarrow B_4\subset B_2\)
\(\Rightarrow B_2\cap B_4=B_4\)
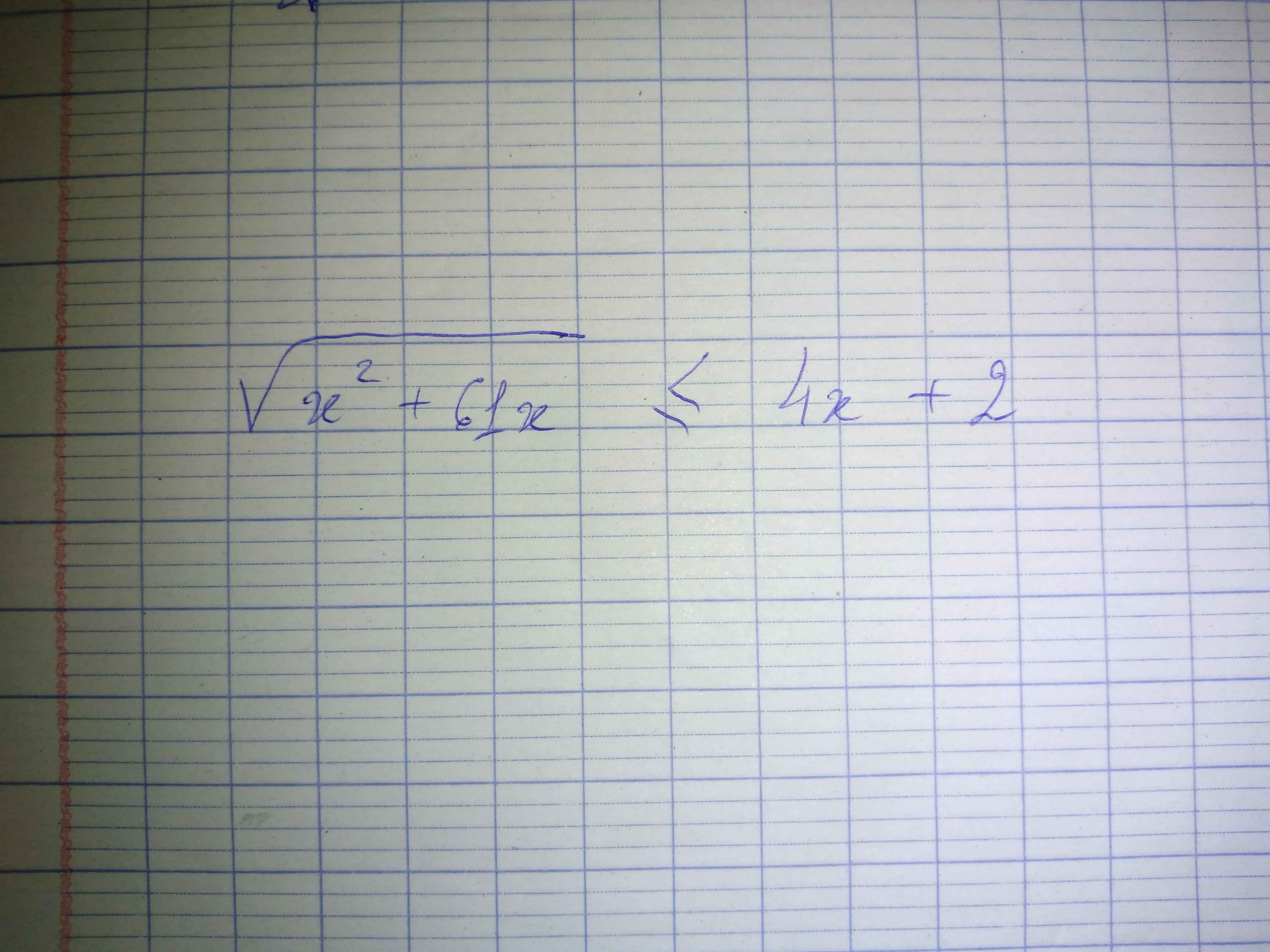
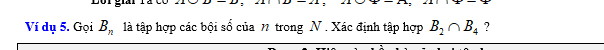
Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
DO đó; OM là tia phân giác của góc AOB
Xét ΔOAM vuông tại A có
\(\tan\widehat{AOM}=\dfrac{AM}{AO}=\sqrt{3}\)
nên \(\widehat{AOM}=60^0\)
=>\(\widehat{AOB}=120^0\)