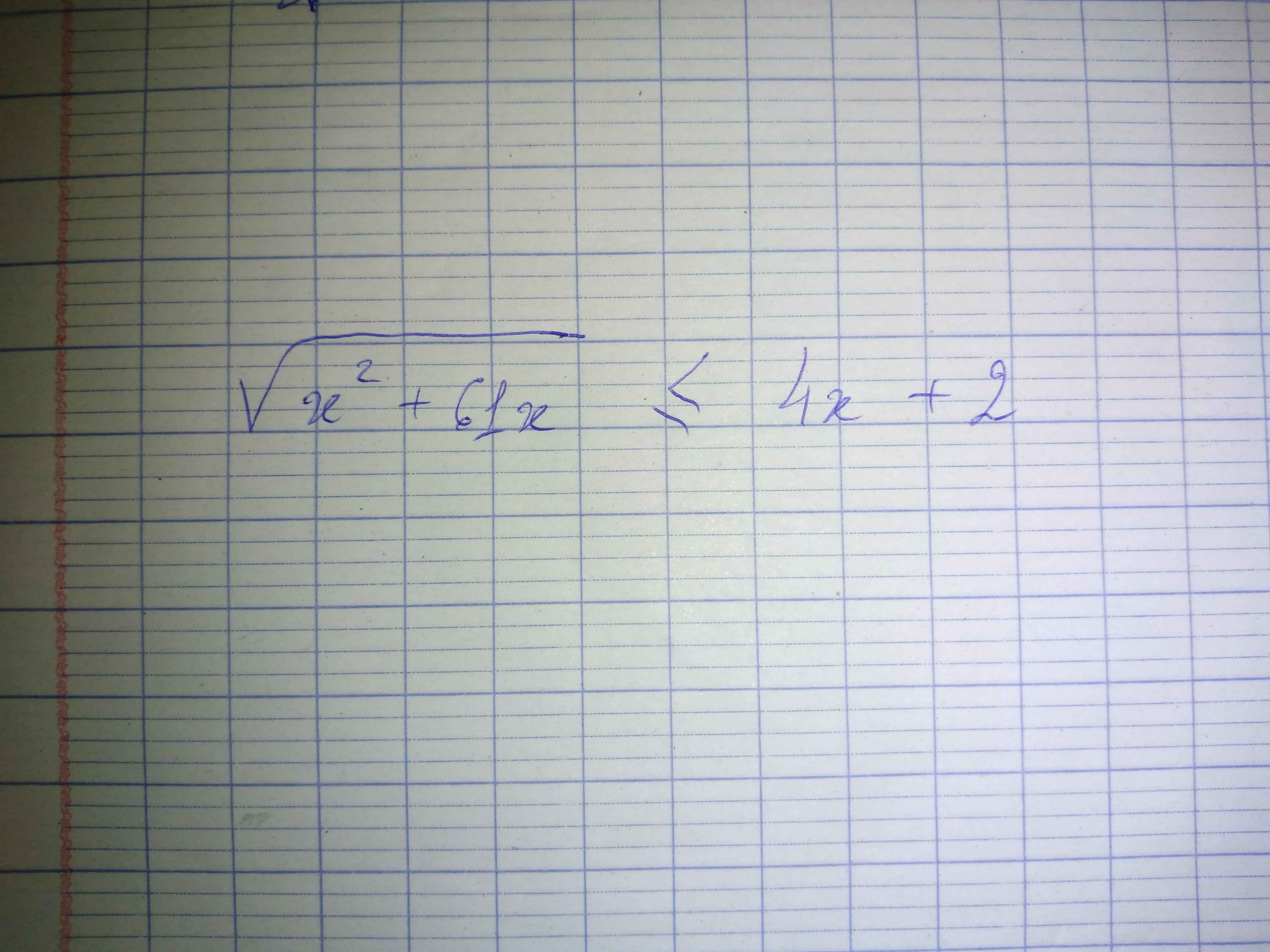Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+61x\ge0\\4x+2\ge0\\x^2+61x\le\left(4x+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge0\\x\le-61\end{matrix}\right.\\x\ge-\dfrac{1}{2}\\15x^2-45x+4\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x\ge\dfrac{45+\sqrt{1785}}{30}\\x\le\dfrac{45-\sqrt{1785}}{30}\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}0\le x\le\dfrac{45-\sqrt{1785}}{30}\\x\ge\dfrac{45+\sqrt{1785}}{30}\end{matrix}\right.\)

1) ĐK: \(x\ge-1\)
\(\sqrt{9x^2+9x+4}>9x+3-\sqrt{x+1}\)
<=> \(\sqrt{9x^2+9x+4}+\sqrt{x+1}>9x+3\)(1)
TH1: 9x + 3 \(\le\)0 <=> x\(\le-\frac{1}{3}\)
(1) luôn đúng
Th2: x\(>-\frac{1}{3}\)
<=> \(\left(\frac{1}{2}x+1-\sqrt{x+1}\right)+\left(\frac{17}{2}x+2-\sqrt{9x^2+9x+4}\right)< 0\)
<=> \(\frac{\frac{1}{4}x^2}{\frac{1}{2}x+1+\sqrt{x+1}}+\frac{\frac{253}{4}x^2}{\frac{17}{2}x+2+\sqrt{9x^2+9x+4}}< 0\)
<=> \(\frac{x^2}{4}\left(\frac{1}{\frac{1}{2}x+1+\sqrt{x+1}}+\frac{253}{\frac{17}{2}x+2+\sqrt{9x^2+9x+4}}\right)< 0\)vô nghiệm
Vì với x \(>-\frac{1}{3}\):
ta có: \(\frac{1}{2}x+1+\sqrt{x+1}>0\)
\(\frac{17}{2}x+2+\sqrt{9x^2+9x+4}=\frac{17}{2}x+2+\sqrt{3\left(x+\frac{1}{2}\right)^2+\frac{7}{4}}>\frac{17}{2}x+2+1>0\)
=> \(\left(\frac{1}{\frac{1}{2}x+1+\sqrt{x+1}}+\frac{253}{\frac{17}{2}x+2+\sqrt{9x^2+9x+4}}\right)>0\)với x \(>-\frac{1}{3}\) và \(x^2\ge0\)với mọi x
=> \(\frac{x^2}{4}\left(\frac{1}{\frac{1}{2}x+1+\sqrt{x+1}}+\frac{253}{\frac{17}{2}x+2+\sqrt{9x^2+9x+4}}\right)\ge0\)với x\(>-\frac{1}{3}\)
Vậy \(x< -\frac{1}{3}\)
Xin lỗi bạn kết luận bài 1 là:
\(-1\le x\le-\frac{1}{3}\)
Bài 2) \(2+\sqrt{x+2}-x\sqrt{x+2}=x\left(\sqrt{x+2}-x\right)\)(2)
ĐK: \(x\ge-2\)
(2) <=> \(2+\sqrt{x+2}+x^2-2x\sqrt{x+2}=0\)
<=> \(8+4\sqrt{x+2}+4x^2-8x\sqrt{x+2}=0\)
<=> \(\left(2x-1\right)^2-4\left(2x-1\right)\sqrt{x+2}+4\left(x+2\right)-1=0\)
<=> \(\left(2x-1-2\sqrt{x+2}\right)^2-1=0\)
<=> \(\left(x-1-\sqrt{x+2}\right)\left(x-\sqrt{x+2}\right)=0\)
<=> \(\orbr{\begin{cases}x-1=\sqrt{x+2}\left(3\right)\\x=\sqrt{x+2}\left(4\right)\end{cases}}\)
(3) <=> \(\hept{\begin{cases}x\ge1\\x^2-3x-1=0\end{cases}}\Leftrightarrow x=\frac{3+\sqrt{13}}{2}\left(tm\right)\)
(4) <=> \(\hept{\begin{cases}x\ge0\\x^2-x-2=0\end{cases}\Leftrightarrow}x=2\left(tm\right)\)
Kết luận:...

\(ĐKXĐ:\hept{\begin{cases}x^2-8x+15\ge0\\x^2+2x-15\ge0\\4x^2-18x+18\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge5\\x\le-5\\x=3\end{cases}}\)
Với x = 8 thì (*) thỏa mãn \(\Rightarrow x=3\)là 1 nghiệm của bất phương trình.
\(\left(^∗\right)\Leftrightarrow\sqrt{\left(x-5\right)\left(x-3\right)}+\sqrt{\left(x+5\right)\left(x-3\right)}\le\sqrt{\left(x-3\right)\left(4x-6\right)}\)(1)
Với \(x\ge5\Rightarrow x-3\ge2>0\)hay \(x-3>0\)thì
\(\left(1\right)\Leftrightarrow\sqrt{x-5}+\sqrt{x+5}\le\sqrt{4x-6}\)\(\Leftrightarrow2x+2\sqrt{x^2-25}\le4x-6\)
\(\Leftrightarrow\sqrt{x^2-25}\le x-3\Leftrightarrow x^2-25=x^2-6x+9\Leftrightarrow x\le\frac{17}{3}\)
\(\Rightarrow5\le x\le\frac{17}{3}\)
Với \(x\le-5\Leftrightarrow-x\ge5\Leftrightarrow3-x\ge8>0\)hay \(x\le-5\Leftrightarrow-x\ge5\Leftrightarrow3-x>0\)thì
\(\left(1\right)\Leftrightarrow\sqrt{\left(5-x\right)\left(3-x\right)}+\sqrt{\left(-5-x\right)\left(3-x\right)}\)
\(\le\sqrt{\left(3-x\right)\left(4-6x\right)}\)
\(\Leftrightarrow\sqrt{5-x}+\sqrt{-x-5}\le\sqrt{6-4x}\)
\(\Leftrightarrow-2x+2\sqrt{\left(5-x\right)\left(-x-5\right)}\le6-4x\)
\(\Leftrightarrow\sqrt{x^2-25}\le3-x\Leftrightarrow x^2-25\le x^2-6x+9\)
\(\Leftrightarrow x\le\frac{17}{3}\Rightarrow x\le-5\)
Từ đó suy ra tập nghiệm của bpt là \(x\in(-\infty;-5]\mu\left\{3\right\}\mu\left[5;\frac{17}{3}\right]\)


1.
a/ ĐKXĐ: \(-1\le x\le5\)
\(\Leftrightarrow\sqrt{x+3}\le\sqrt{5-x}+\sqrt{x+1}\)
\(\Leftrightarrow x+3\le6+2\sqrt{\left(5-x\right)\left(x+1\right)}\)
\(\Leftrightarrow x-3\le2\sqrt{-x^2+4x+5}\)
- Với \(x< 3\Rightarrow\left\{{}\begin{matrix}VT< 0\\VP\ge0\end{matrix}\right.\) BPT luôn đúng
- Với \(x\ge3\) cả 2 vế ko âm, bình phương:
\(x^2-6x+9\le-4x^2+16x+20\)
\(\Leftrightarrow5x^2-22x-11\le0\) \(\Rightarrow\frac{11-4\sqrt{11}}{5}\le x\le\frac{11+4\sqrt{11}}{5}\)
\(\Rightarrow3\le x\le\frac{11+4\sqrt{11}}{5}\)
Vậy nghiệm của BPT đã cho là \(-1\le x\le\frac{11+4\sqrt{11}}{5}\)
1b/
Đặt \(\sqrt{2x^2+8x+12}=t\ge2\)
\(\Rightarrow x^2+4x=\frac{t^2}{2}-6\)
BPT trở thành:
\(\frac{t^2}{2}-12\ge t\Leftrightarrow t^2-2t-24\ge0\) \(\Rightarrow\left[{}\begin{matrix}t\le-4\left(l\right)\\t\ge6\end{matrix}\right.\)
\(\Rightarrow\sqrt{2x^2+8x+12}\ge6\)
\(\Leftrightarrow2x^2+8x-24\ge0\Rightarrow\left[{}\begin{matrix}x\le-6\\x\ge2\end{matrix}\right.\)