Giúp em câu này vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giúp em 2 câu này vs ạ
31 tháng 12 2023
Câu 4:
a: ĐKXĐ: \(x\notin\left\{\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
b: \(A=\dfrac{1-2x}{1-4x^2}\)
\(=\dfrac{1-2x}{\left(1-2x\right)\left(1+2x\right)}\)
\(=\dfrac{1}{2x+1}\)
c: Để A là số nguyên thì \(2x+1\inƯ\left(1\right)\)
=>\(2x+1\in\left\{1;-1\right\}\)
=>\(2x\in\left\{0;-2\right\}\)
=>\(x\in\left\{0;-1\right\}\)
Câu 3:
a: \(A=\dfrac{3x-2}{x}-\dfrac{x-7}{x-5}-\dfrac{10}{x^2-5x}\)
\(=\dfrac{3x-2}{x}-\dfrac{x-7}{x-5}-\dfrac{10}{x\left(x-5\right)}\)
\(=\dfrac{\left(3x-2\right)\left(x-5\right)-x\cdot\left(x-7\right)-10}{x\left(x-5\right)}\)
\(=\dfrac{3x^2-17x+10-x^2+7x-10}{x\left(x-5\right)}\)
\(=\dfrac{2x^2-10x}{x\left(x-5\right)}=\dfrac{2x\left(x-5\right)}{x\left(x-5\right)}=2\)
giúp em bài này vs ạ em cảm ơn trc ạ
9 tháng 10 2021
a) \(A=x^4+4x+7=\left(x^2+4x+4\right)+3=\left(x+2\right)^2+3\ge3\)
\(minA=3\Leftrightarrow x=-2\)
b) \(B=x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(minB=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
\(maxC=7\Leftrightarrow x=2\)
d) \(D=2x-2x^2-5=-2\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{9}{2}=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{2}\le-\dfrac{9}{2}\)
\(maxD=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{1}{2}\)
LM
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
2
10 tháng 11 2021
\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
8 tháng 3 2022
a: =>(3x+1)(3x-1)-(3x+1)(2x-3)=0
=>(3x+1)(3x-1-2x+3)=0
=>(3x+1)(x+2)=0
=>x=-1/3 hoặc x=-2
b: =>(3x+1)(6x+2)-(3x+1)(x-2)=0
=>(3x+1)(6x+2-x+2)=0
=>(3x+1)(5x+4)=0
=>x=-1/3 hoặc x=-4/5
cứu em 2 câu này vs ạ
31 tháng 12 2023
Câu 2:
a: *Vẽ đồ thị
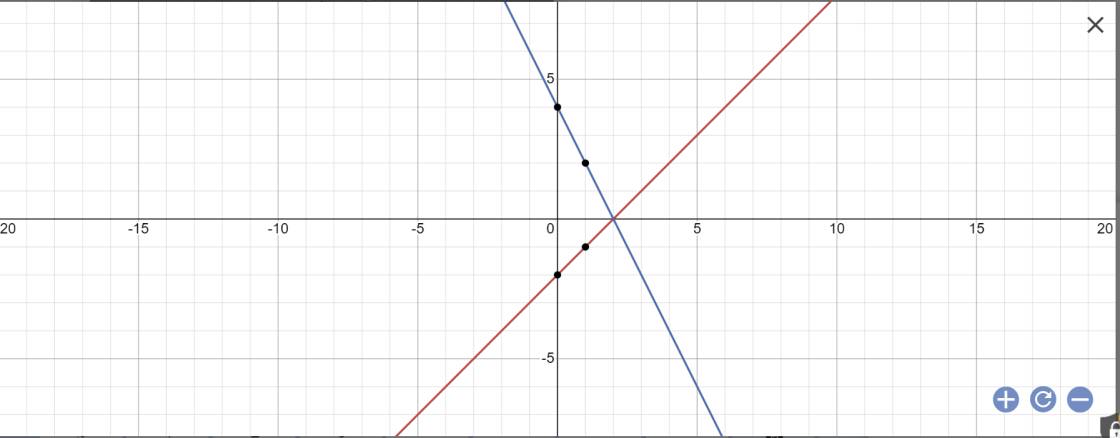
*Tìm giao điểm:
Phương trình hoành độ giao điểm là:
x-2=-2x+4
=>x+2x=4+2
=>3x=6
=>x=2
Thay x=2 vào y=x-2, ta được:
y=2-2=0
Vậy: (d1):y=x-2 cắt (d2): y=-2x+4 tại A(2;0)
b: *Vẽ đồ thị
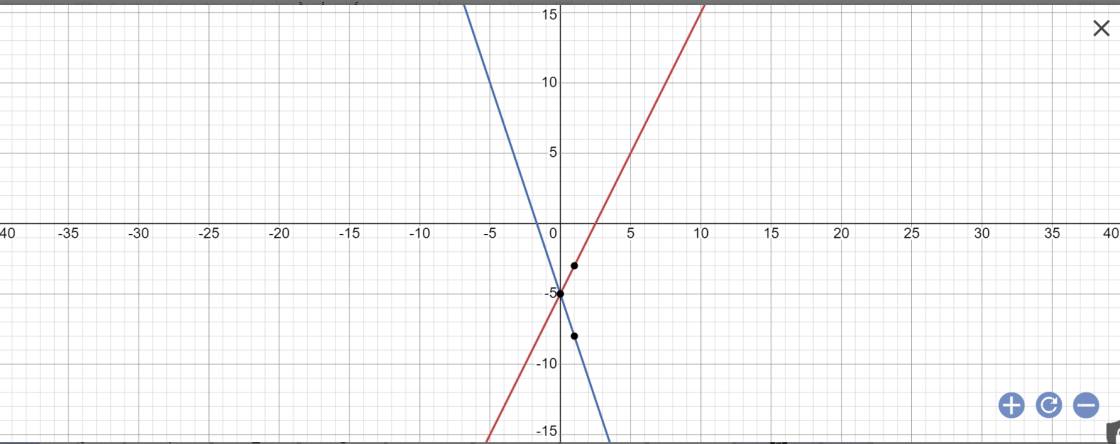
*Tìm giao điểm
Phương trình hoành độ giao điểm là:
2x-5=-3x-5
=>2x+3x=-5+5=0
=>5x=0
=>x=0
Thay x=0 vào y=2x-5, ta được:
\(y=2\cdot0-5=-5\)
Vậy: (d1): y=2x-5 cắt (d2):y=-3x-5 tại A(0;-5)
c: *Vẽ đồ thị
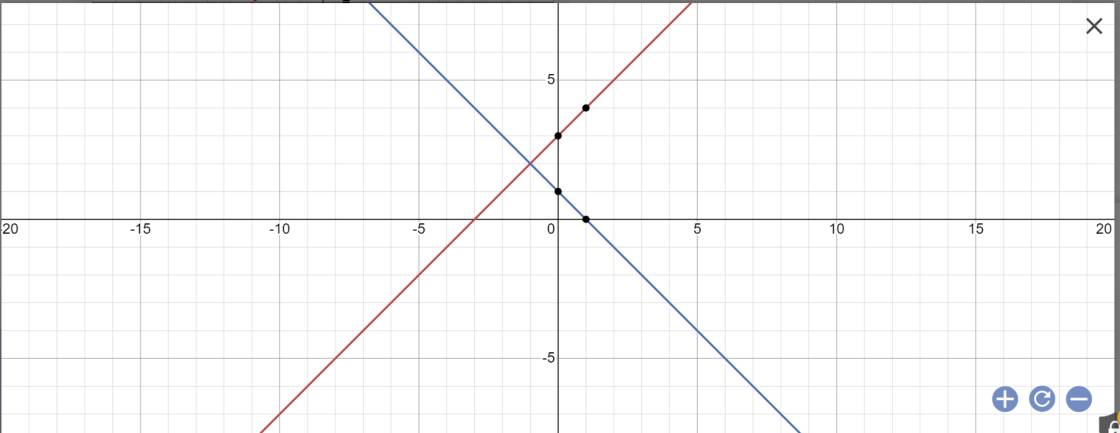
*Tìm giao điểm
Phương trình hoành độ giao điểm là:
x+3=-x+1
=>x+x=1-3
=>2x=-2
=>x=-1
Thay x=-1 vào y=x+3, ta được:
y=-1+3=2
vậy: (d1): y=x+3 và (d2): y=-x+1 cắt nhau tại C(-1;2)
KV
9 tháng 5 2023
Câu 1. B
Câu 2. C
Câu 3. C
Câu 4. A
Câu 5. B
Câu 6. C
Câu 7. A
Câu 8. D
giúp em mấy bài này vs ạ
21 tháng 3 2023
1:
a: ĐKXĐ: x<>0; x<>5; x<>-5
\(A=\dfrac{x^2-5x+5x+25+10x}{\left(x-5\right)\left(x+5\right)}\cdot\dfrac{x-5}{x}\)
\(=\dfrac{x^2+10x+25}{x+5}\cdot\dfrac{1}{x}=\dfrac{x+5}{x}\)
b: Để A>0 và A nguyên thì 5 chia hết cho x và x>0
=>x=1
\(=12,7\left(85+15\right)=12,7\cdot100=1270\)