
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(b,\dfrac{1}{2}+\dfrac{13}{19}-\dfrac{4}{9}+\dfrac{6}{19}+\dfrac{5}{18}\\ =\left(\dfrac{1}{2}+\dfrac{5}{18}\right)+\left(\dfrac{13}{19}+\dfrac{6}{19}\right)-\dfrac{4}{9}\\ =\left(\dfrac{9}{18}+\dfrac{5}{18}\right)+\dfrac{19}{19}-\dfrac{4}{9}\\ =\dfrac{14}{18}+1-\dfrac{4}{9}\\ =\dfrac{7}{9}+1-\dfrac{4}{9}\\ =\left(\dfrac{7}{9}-\dfrac{4}{9}\right)+1\\ =\dfrac{3}{9}+1\\ =\dfrac{1}{3}+1\\ =\dfrac{4}{3}\)
\(c,\dfrac{-20}{23}+\dfrac{2}{3}-\dfrac{3}{23}+\dfrac{2}{5}+\dfrac{7}{15}\\ =\left(-\dfrac{20}{23}-\dfrac{3}{23}\right)+\left(\dfrac{2}{5}+\dfrac{7}{15}\right)+\dfrac{2}{3}\\ =-\dfrac{23}{23}+\left(\dfrac{6}{15}+\dfrac{7}{15}\right)+\dfrac{2}{3}\\ =-1+\dfrac{13}{15}+\dfrac{2}{3}\\ =-\dfrac{15}{15}+\dfrac{13}{15}+\dfrac{10}{15}\\ =\dfrac{8}{15}\)
\(e,\dfrac{5}{7}.\dfrac{5}{11}+\dfrac{5}{7}.\dfrac{2}{11}-\dfrac{5}{7}.\dfrac{14}{11}\\ =\dfrac{5}{7}.\left(\dfrac{5}{11}+\dfrac{2}{11}-\dfrac{14}{11}\right)\\ =\dfrac{5}{7}.\dfrac{-7}{11}\\ =-\dfrac{35}{77}\\ =-\dfrac{5}{11}\)
\(f,\dfrac{2}{11}.\dfrac{-5}{4}+\dfrac{-9}{11}.\dfrac{5}{4}+1\dfrac{3}{4}\\ =-\dfrac{2}{11}.\dfrac{5}{4}+\dfrac{-9}{11}.\dfrac{5}{4}+\dfrac{7}{4}\\=\dfrac{5}{4}.\left(-\dfrac{2}{11}+\dfrac{-9}{11}\right)+\dfrac{7}{4}\\ =\dfrac{5}{4}.1+\dfrac{7}{4}\\ =\dfrac{5}{4}+\dfrac{7}{4}\\=\dfrac{12}{4}\\ =3\)
\(h,\dfrac{7}{4}\cdot\dfrac{29}{5}-\dfrac{7}{5}\cdot\dfrac{9}{4}+3\dfrac{2}{13}\\ =\dfrac{7}{4}\cdot\dfrac{29}{5}-\dfrac{7}{4}\cdot\dfrac{9}{5}+\dfrac{41}{13}\\ =\dfrac{7}{4}\cdot\left(\dfrac{29}{5}-\dfrac{9}{5}\right)+\dfrac{41}{13}\\ =\dfrac{7}{4}\cdot\dfrac{20}{5}+\dfrac{41}{13}\\ =\dfrac{7}{4}.4+\dfrac{41}{13}\\ =\dfrac{28}{4}+\dfrac{41}{13}\\ =7+\dfrac{41}{13}\\ =\dfrac{132}{13}\)

(a) \(A=\dfrac{3}{x-2}\in Z\)
\(\Rightarrow\left(x-2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\\x=4\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{-2;0;2;4\right\}.\)
(b) \(B=-\dfrac{11}{2x-3}\in Z\)
\(\Rightarrow\left(2x-3\right)\inƯ\left(11\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=1\\2x-3=-1\\2x-3=11\\2x-3=-11\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=7\\x=-4\end{matrix}\right.\)
Vậy: \(x\in\left\{-4;1;2;7\right\}.\)
(c) \(C=\dfrac{x+3}{x+1}=\dfrac{\left(x+1\right)+2}{x+1}=1+\dfrac{2}{x+1}\in Z\Rightarrow\dfrac{2}{x+1}\in Z\)
\(\Rightarrow\left(x+1\right)\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x+1=1\\x+1=-1\\x+1=2\\x+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=1\\x=-3\end{matrix}\right.\)
Vậy: \(x\in\left\{-3;-2;0;1\right\}.\)
(d) \(D=\dfrac{2x+10}{x+3}=\dfrac{2\left(x+3\right)+4}{x+3}=2+\dfrac{4}{x+3}\in Z\Rightarrow\dfrac{4}{x+3}\in Z\)
\(\Rightarrow\left(x+3\right)\inƯ\left(4\right)=\left\{\pm1;\pm2\pm4\right\}\)
\(\Rightarrow x\in\left\{-2;-4;-1;-5;1;-7\right\}\)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

a) Trong cùng phía
b) đồng vị
c) so le trong
d) so le trong
e) trong cùng phía

Ta có: \(5^x+25\cdot5^{x+1}-125\cdot5^{x+2}=-74975\)
\(\Leftrightarrow5^x+25\cdot5^x\cdot5-125\cdot25\cdot5^x=-74975\)
\(\Leftrightarrow5^x\cdot\left(1+125-3125\right)=-74975\)
\(\Leftrightarrow5^x=25\)
hay x=2
Vậy: x=2

Đây là lịch sử không phải Toán, bạn nên để đúng chủ đề bài học nhé.
mình biết là mình hỏi sai môn ạ
nma mình cũng đã gửi thử một câu hỏi bên phía lịch sử rồi ạ nhưng chưa có trl(T-T)
mình lên mạng tham khảo thì ko có phần nhận xét(T-T)

a, M(x)= 3x^3 - 2x^2 + 1 (đã rút gọn ) , ý b bạn chỉ cần thay M(-1) và M(2) vào x lần lượt từng con là đc vd : M(-1)= 3* (-1^3) - 2* (- 1)^2 + 1 rồi tính ra kết quả là được

6:
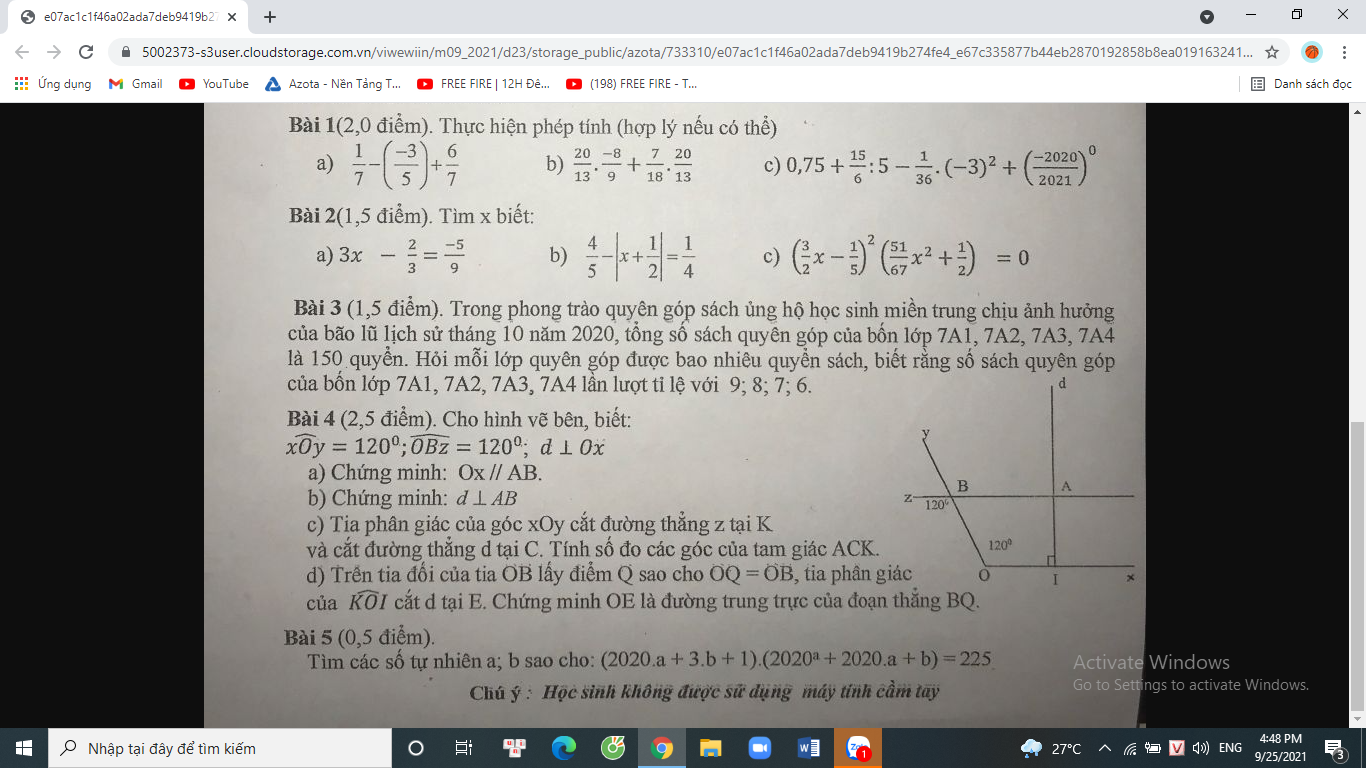
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2
 giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước
giúp em với ạ em đang cần gấp lắm ạ em cảm ơn trước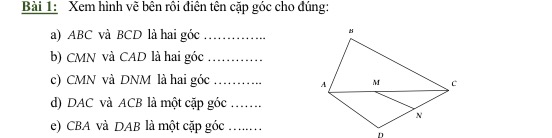


 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
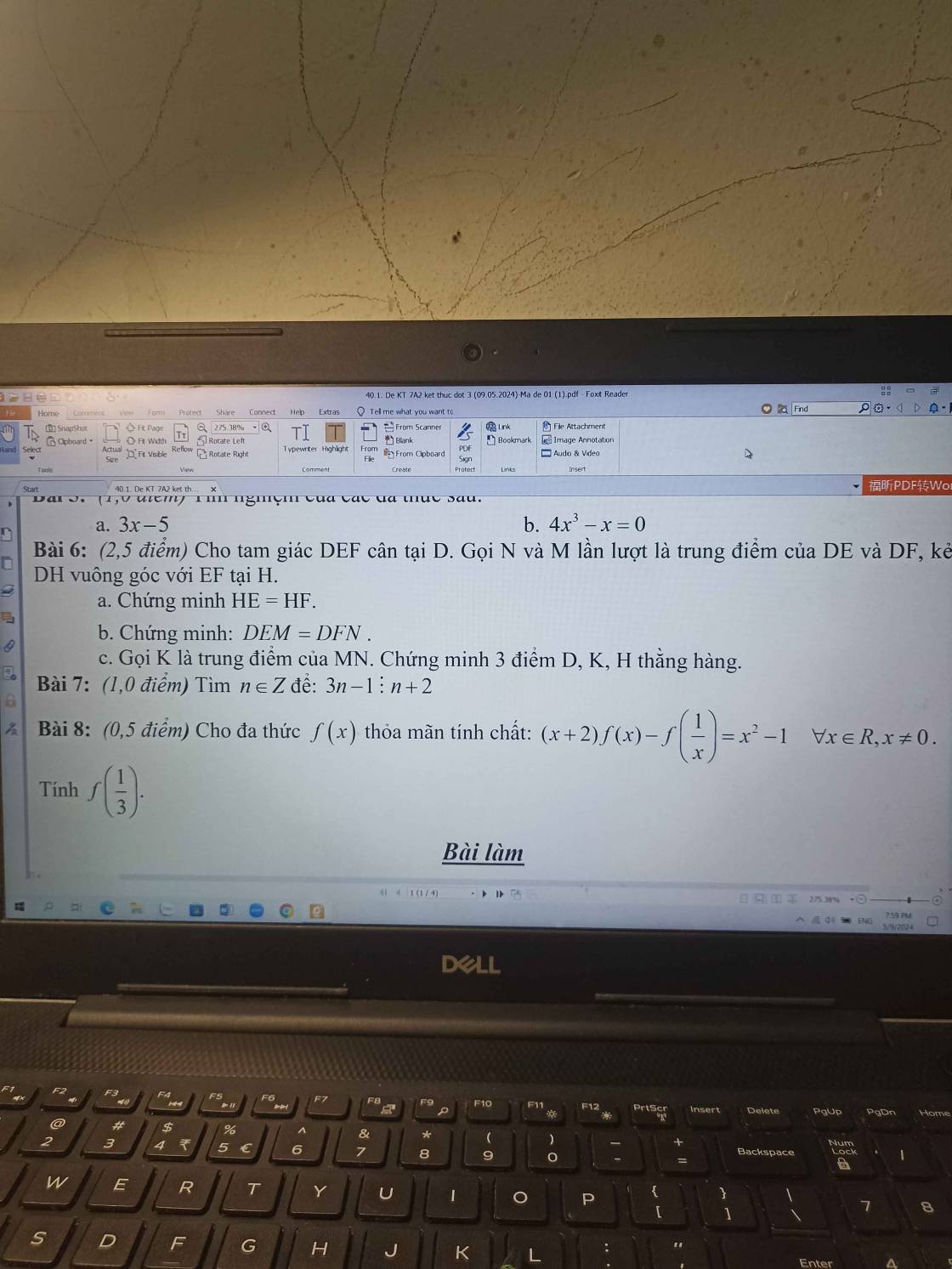
Bài 8:
Thay x=3 vào phương trình, ta được:
\(\left(3+2\right)\cdot f\left(3\right)-f\left(\dfrac{1}{3}\right)=3^2-1\)
=>\(5\cdot f\left(3\right)-f\left(\dfrac{1}{3}\right)=8\left(1\right)\)
Thay x=1/3 vào phương trình, ta được:
\(\left(\dfrac{1}{3}+2\right)\cdot f\left(\dfrac{1}{3}\right)-f\left(3\right)=\left(\dfrac{1}{3}\right)^2-1\)
=>\(\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)-f\left(3\right)=-\dfrac{8}{9}\)
=>\(f\left(3\right)-\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)=\dfrac{8}{9}\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}5\cdot f\left(3\right)-f\left(\dfrac{1}{3}\right)=8\\f\left(3\right)-\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)=\dfrac{8}{9}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{35}{3}\cdot f\left(3\right)-\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)=\dfrac{56}{3}\\f\left(3\right)-\dfrac{7}{3}\cdot f\left(\dfrac{1}{3}\right)=\dfrac{8}{9}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{32}{3}\cdot f\left(3\right)=\dfrac{56}{3}-\dfrac{8}{9}=\dfrac{160}{9}\\5\cdot f\left(3\right)-f\left(\dfrac{1}{3}\right)=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}f\left(3\right)=\dfrac{5}{3}\\f\left(\dfrac{1}{3}\right)=5\cdot\dfrac{5}{3}-8=\dfrac{25}{3}-8=\dfrac{1}{3}\end{matrix}\right.\)
vậy: \(f\left(\dfrac{1}{3}\right)=\dfrac{1}{3}\)