
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: \(A=8\sqrt{2}-15\sqrt{2}-8\sqrt{2}=-15\sqrt{2}\)
b: \(B=-\sqrt{7}\)
Bài 1:
\(A=8\sqrt{2}-15\sqrt{2}-8\sqrt{2}=-15\sqrt{2}\\ B=\dfrac{-\sqrt{7}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}=-\sqrt{7}\\ C=\sqrt{\left(\sqrt{2}+\sqrt{5}\right)^2}-\sqrt{5}=\sqrt{2}+\sqrt{5}-\sqrt{5}=\sqrt{2}\)
Bài 2:
\(a,\Leftrightarrow x+2=9\Leftrightarrow x=7\\ b,ĐK:x\ge-5\\ PT\Leftrightarrow2\sqrt{x+5}-6\sqrt{x+5}=-16\\ \Leftrightarrow\sqrt{x+5}=\dfrac{-16}{-4}=4\\ \Leftrightarrow x+5=16\\ \Leftrightarrow x=11\left(tm\right)\)
Bài 4:
Gọi góc đó là \(\alpha\) thì \(\sin\alpha=\dfrac{6}{8}\approx\sin49^0\Leftrightarrow\alpha\approx49^0\)
Vậy góc tạo bởi thang và mặt đất xấp xỉ 49 độ

a.
\(\Delta=\left(-5\right)^2-4.3.2=25-24=1>0\)
\(\Rightarrow\) Phương trình có 2 nghiệm pb
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{5}{3}\\x_1x_2=\dfrac{2}{3}\end{matrix}\right.\)
\(4A=x_1^2+x_2^2-x_1x_2=\left(x_1^2+x_2^2+2x_1x_2\right)-3x_1x_2\)
\(4A=\left(x_1+x_2\right)^2-3x_1x_2\)
\(4A=\left(\dfrac{5}{3}\right)^2-3.\left(\dfrac{2}{3}\right)=\dfrac{7}{9}\)
\(\Rightarrow A=\dfrac{7}{36}\)


\(a,B=4\sqrt{x+1}-3\sqrt{x+1}+\sqrt{x+1}+2\sqrt{x+1}=4\sqrt{x+1}\\ b,B=8\Leftrightarrow4\sqrt{x+1}=8\\ \Leftrightarrow\sqrt{x+1}=2\\ \Leftrightarrow x+1=4\\ \Leftrightarrow x=3\left(tm\right)\)


Pt hoành độ giao điểm:
\(x^2=mx+3-m\Leftrightarrow x^2-mx+m-3=0\)
\(\Delta=m^2-4\left(m-3\right)=\left(m-2\right)^2+8>0\) ; \(\forall m\)
\(\Rightarrow\) (d) luôn cắt (P) tại 2 điểm pb
Giả sử hoành độ của 2 giao điểm lần lượt là \(x_1< x_2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-3\end{matrix}\right.\)
M nằm giữa 2 giao điểm khi và chỉ khi: \(x_1< x_M< x_2\)
\(\Leftrightarrow x_1< 1< x_2\Leftrightarrow\left(x_1-1\right)\left(x_2-1\right)< 0\)
\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1< 0\)
\(\Leftrightarrow-2< 0\) (luôn đúng)
Vậy (d) cắt (P) tại 2 điểm nằm về 2 phía của M với mọi m

Do (d) đi qua C và D, thay tọa độ C và D vào pt (d) ta được:
\(\left\{{}\begin{matrix}a.\left(-1\right)+b=1\\a.\left(-2\right)+b=-3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\-2a+b=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=5\end{matrix}\right.\)
Phương trình (d) có dạng: \(y=4x+5\)

Do (d) đi qua E và G nên thay tọa độ E và G vào pt (d) ta được:
\(\left\{{}\begin{matrix}a.1+b=-3\\a.\left(-2\right)+b=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a+b=-3\\-2a+b=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a=-9\\-2a+b=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-3\\b=0\end{matrix}\right.\)
Vậy pt (d) là: \(y=-3x\)

b: \(Q=\dfrac{x+5}{\sqrt{x}+2}=\dfrac{x-4}{\sqrt{x}+2}+\dfrac{9}{\sqrt{x}+2}=\sqrt{x}-2+\dfrac{9}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4\)
\(\Leftrightarrow Q\ge2\sqrt{9}-4=2\cdot3-4=2\)
Dấu '=' xảy ra khi x=1


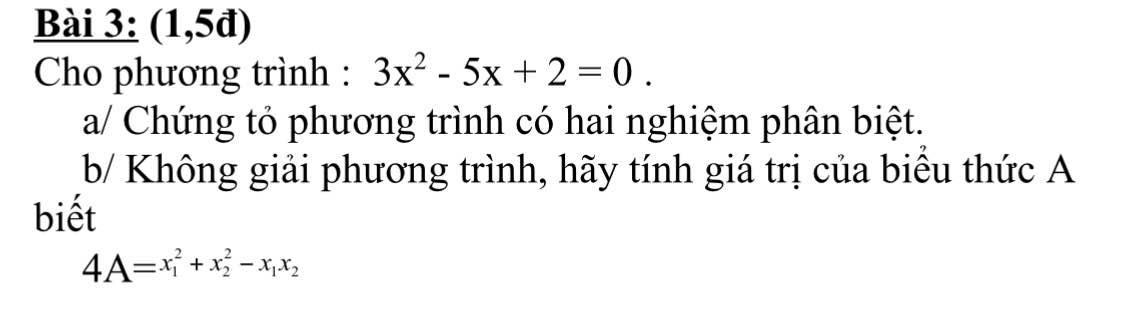




c) \(\left(\dfrac{\sqrt{x}}{2\sqrt{x}-2}-\dfrac{\sqrt{x}}{2\sqrt{x}+2}\right):\dfrac{\sqrt{x}}{x+2\sqrt{x}+1}\)
= \(\left(\dfrac{\sqrt{x}}{2\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}}{2\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}}{\sqrt{x}^2+2\sqrt{x}+1^2}\)
= \(\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\) \(:\dfrac{\sqrt{x}}{\left(\sqrt{x}+1\right)^2}\)
= \(\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-\sqrt{x}\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\) \(.\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}\)
= \(\dfrac{2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}\)
= \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
Chúc bạn học tốt