
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(c,ĐK:x\ge2\\ PT\Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\\ \Leftrightarrow4\sqrt{x-2}=40\\ \Leftrightarrow\sqrt{x-2}=10\\ \Leftrightarrow x-2=100\Leftrightarrow x=102\left(tm\right)\)
\(c,\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\) (Điều kiện: \(x\ge2\))
\(\Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)
\(\Leftrightarrow4\sqrt{x-2}=40\)
\(\Leftrightarrow\sqrt{x-2}=10\)
\(\Leftrightarrow x-2=100\)
\(\Leftrightarrow x=102\) (thỏa mãn điều kiện)
Vậy: \(S=\left\{102\right\}\)

\(A=\dfrac{\left(\sqrt{x}-3\right)^2}{\sqrt{x}-3}+\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\sqrt{x}+3}=\sqrt{x}-3+\sqrt{x}=2\sqrt{x}-3\)



a: \(P=\left(\dfrac{3\sqrt{a}-3}{\sqrt{a}\left(\sqrt{a}+1\right)}\right)\cdot\dfrac{\left(\sqrt{a}+1\right)^2}{\sqrt{a}-1}\)
\(=\dfrac{3\sqrt{a}+3}{\sqrt{a}}\)





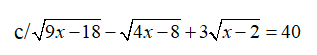




 làm cụ thể giúp mình vớiii
làm cụ thể giúp mình vớiii
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{4}{5y}=7\\\dfrac{3}{4x}-\dfrac{2}{5y}=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{4}{5y}=7\\\dfrac{6}{4x}-\dfrac{4}{5y}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{6}{4x}=7+6\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2}{3x}+\dfrac{3}{2x}=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}\left(\dfrac{2}{3}+\dfrac{3}{2}\right)=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}\cdot\dfrac{13}{6}=13\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{x}=13:\dfrac{13}{6}=6\\\dfrac{2}{3x}+\dfrac{4}{5y}=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\\dfrac{4}{5y}=7-\dfrac{2}{3x}=7-\dfrac{2}{3\cdot\dfrac{1}{6}}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{6}\\\dfrac{4}{5y}=7-\dfrac{2}{\dfrac{1}{2}}=7-2\cdot2=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{6}\\5y=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\y=\dfrac{4}{15}\end{matrix}\right.\left(nhận\right)\)