K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
K
2
5 tháng 3 2022
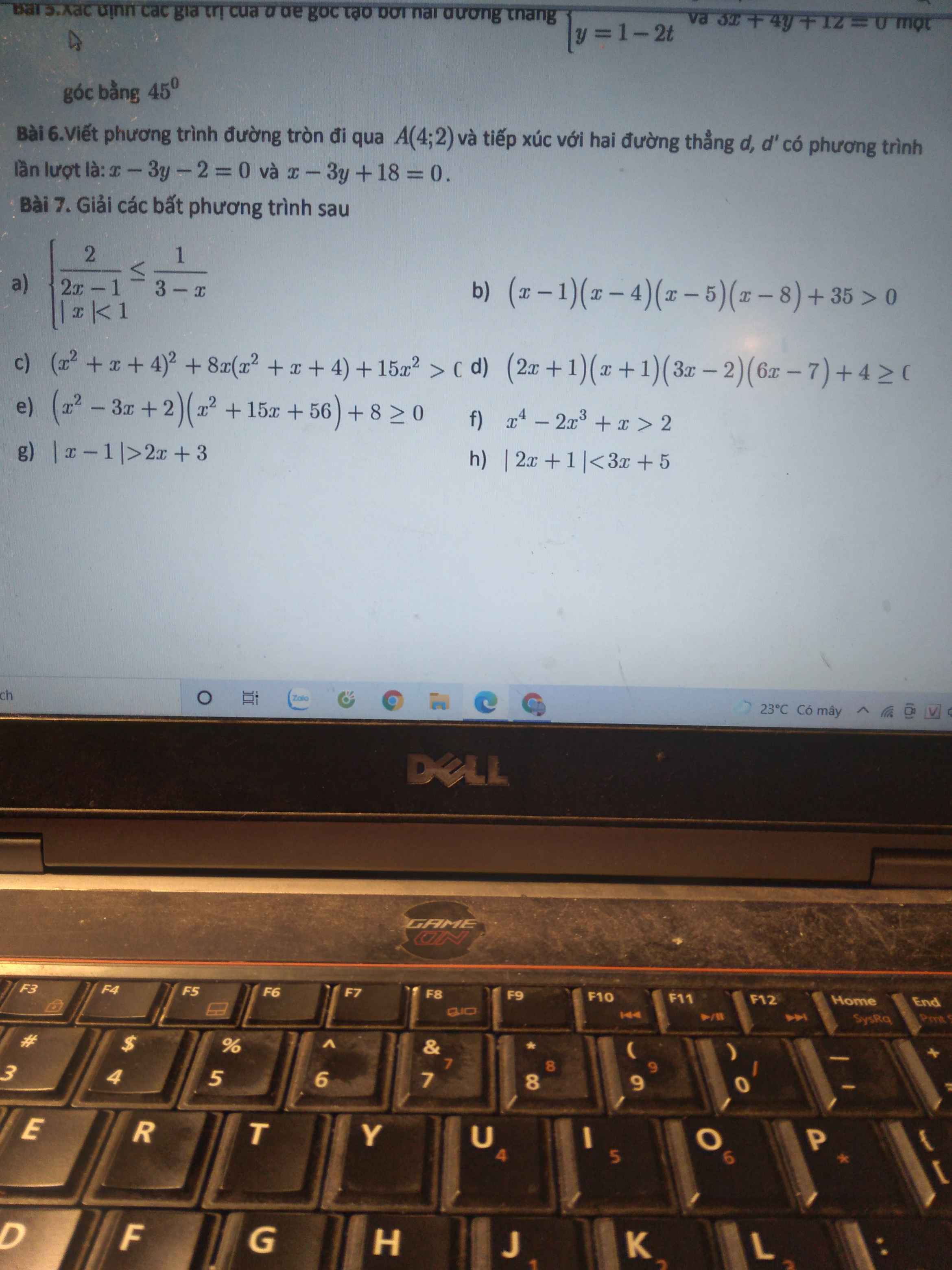
\(\left(x\ne3;x\ne\dfrac{1}{2}\right)\)\(\left\{{}\begin{matrix}\dfrac{2}{2x-1}\le\dfrac{1}{3-x}\\\left|x\right|< 1\Leftrightarrow-1< x< 1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2\left(3-x\right)-2x+1}{\left(2x-1\right)\left(3-x\right)}\le0\left(1\right)\\-1< x< 1\end{matrix}\right.\)\(\)
\(\left(1\right)\Leftrightarrow\dfrac{-4x+7}{\left(2x-1\right)\left(3-x\right)}\le0\)\(\Leftrightarrow\dfrac{-4x+7}{-2x^2+7x-3}\le0\Leftrightarrow x\in\left(-\infty;\dfrac{1}{2}\right)\cup[\dfrac{7}{4};3)\)
\(kết\) \(hợp:-1< x< 1\)\(\Rightarrow x\in\left(-1;\dfrac{1}{2}\right)\cup[\dfrac{7}{4};3)\)
\(b,\)\(\left(x-1\right)\left(x-4\right)\left(x-5\right)\left(x-8\right)+35>0\)
\(\Leftrightarrow\left(x^2-9x+8\right)\left(x^2-9x+20\right)+35>0\)
\(đặt:x^2-9x+8=t\ge-\dfrac{49}{4}\)
\(bpt\Leftrightarrow t\left(t+12\right)+35>0\Leftrightarrow t^2+12t+35>0\Leftrightarrow\left[{}\begin{matrix}t< -7\\t>-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-9x+8< -7\\x^2-9x+8>-5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{9-\sqrt{21}}{2}< x< \dfrac{9+\sqrt{21}}{2}\\x\in\left(-\infty;\dfrac{9-\sqrt{29}}{2}\right)\cup\left(\dfrac{9+\sqrt{29}}{2};+\infty\right)\end{matrix}\right.\)
\(c;\)\(\left(x^2+x+4\right)^2+2.4x\left(x^2+x+4\right)+16x^2-x^2>0\)
\(\Leftrightarrow\left(x^2+x+4+4x\right)^2-x^2>0\)
\(\Leftrightarrow\left(x+2\right)^2\left(x^2+6x+4\right)>0\)
\(\Leftrightarrow x^2+6x+4>0\Leftrightarrow....\)
ý d; giống ý b
\(e;bpt\Leftrightarrow\left(x-2\right)\left(x-1\right)\left(x+7\right)\left(x+8\right)+8>0\)
\(\Leftrightarrow\left(x^2+6x-16\right)\left(x^2+6x-7\right)+8>0\)
\(đặt:x^2+6x-7=t\ge-16\Rightarrow t\left(t-9\right)+8>0\)
(làm giống ý b)
\(f;x^4-2x^3+x-2>0\Leftrightarrow\left(x+1\right)\left(x-2\right)\left(x^2-x+1\right)>0\left(do:x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\right)\)
\(\Rightarrow bpt\Leftrightarrow\left(x+1\right)\left(x-2\right)>0\Leftrightarrow\left[{}\begin{matrix}x< -1\\x>2\end{matrix}\right.\)
\(g;h\) dùng bảng phá giá trị tuyệt đối để làm
NT
1
21 tháng 6 2023
Cái này bạn quy đồng lên thôi
\(\dfrac{pi}{3}+\dfrac{kpi}{3}=\dfrac{2pi}{6}+\dfrac{k2pi}{6}=\dfrac{k2pi+2pi}{6}=\dfrac{\left(k+1\right)\cdot2pi}{6}\)
Do là k2pi và (k+1)2pi là hai điểm trùng nhau nên được tính chung luôn là k2pi bạn nha
Câu 21: B
Câu 22: C
Câu 23: A
Câu 24: D
Câu 25: B
Câu 26: A
Câu 27: B
Câu 28: A
Câu 29: C
Câu 30: C
Câu 31: A
Câu 32: A