
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1.
a.Áp dụng tính chất đường phân giác, ta có:
\(\dfrac{AB}{AH}=\dfrac{BC}{CH}\)
\(\Leftrightarrow\dfrac{6}{8}=\dfrac{BC}{CH}\)
\(\Leftrightarrow\dfrac{CH}{8}=\dfrac{BC}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{CH+BC}{8+6}=\dfrac{10}{14}=\dfrac{5}{7}\)
\(CH=\dfrac{5}{7}.8=\dfrac{40}{7}\)
\(BC=\dfrac{5}{7}.6=\dfrac{30}{7}\)
b.\(\Delta ABH\) là tam giác vuông vì:
\(HB^2=AB^2+AH^2\)
\(\Leftrightarrow10^2=6^2+8^2\) ( pitago đảo )
Áp dụng định lý pitago vào tam giác vuông ACB
\(AB^2=BC^2+AC^2\)
\(\Rightarrow AC=\sqrt{6^2-\dfrac{30}{7}^2}=\dfrac{12\sqrt{6}}{7}\)
\(S_{ABC}=\dfrac{1}{2}.BC.AC=\dfrac{1}{2}.\dfrac{30}{7}.\dfrac{12\sqrt{6}}{7}\simeq8,998cm^2\)
\(S_{ACH}=\dfrac{1}{2}.HC.AC=\dfrac{1}{2}.\dfrac{40}{7}.\dfrac{12\sqrt{6}}{7}\simeq11,997cm^2\)

Xét ΔABC có BD là phân giác
nên AB/AD=BC/CD
=>AB/4=BC/5
Đặt AB/4=BC/5=k
=>AB=4k; BC=5k
Theo đề, ta có: \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow9k^2=81\)
=>k=3
=>AB=12; BC=15
Vì BD là phân giác của \(\widehat{ABC}\) nên \(\dfrac{AD}{AB}=\dfrac{DC}{BC}\Leftrightarrow\dfrac{4}{AB}=\dfrac{5}{BC}\Leftrightarrow BC=\dfrac{5AB}{4}\)
Có : AC=AD+DC=4+5=9cm
Xét \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\) ( định lí Pi-ta-go)
\(AB^2+81=\dfrac{25AB^2}{16}\)
\(81=\dfrac{25AB^2}{16}-\dfrac{16AB^2}{16}\)
\(\Leftrightarrow\dfrac{9AB^2}{16}=81\)
\(9AB^2=1296\)
\(AB^2=144\)
AB=12 cm
Có : \(BC=\dfrac{5AB}{4}=\dfrac{5.12}{4}=15cm\)

a:Xét ΔAMN có MB là tia phân giác
nên AB/BN=AM/MN=AN/MN(1)
Xét ΔAMN có NC là tia phân giác
nên AC/CM=AN/MN(2)
Từ (1) và (2) suy ra AB/BN=AC/CM
hay BC//MN
b: Xét ΔCBM có \(\widehat{CBM}=\widehat{CMB}\)
nên ΔCBM cân tại C
=>CB=CM=6cm
Xét ΔABC có BC//MN
nên BC/MN=AC/AM
\(\Leftrightarrow\dfrac{AC}{AC+6}=\dfrac{1}{2}\)
=>AC=6(cm)
=>AM=12(cm)

Câu 1:
a: x/1.25=3.5/2.5=7/5
=>x=1.75
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{x+y}{4+3}=\dfrac{2.1}{7}=0.3\)
Do đó: x=1,2; y=0,9

a, \(3x+7x^2+5+2x-7x^2\ge0\Leftrightarrow5x+5\ge0\Leftrightarrow x\ge-1\)
b, \(12x\ge-16\Leftrightarrow x\ge-\dfrac{4}{3}\)
c, \(\dfrac{5x-1-6}{6}-\dfrac{4\left(x+1\right)}{3}\le0\)
\(\Leftrightarrow\dfrac{5x-7-8\left(x+1\right)}{6}\le0\Rightarrow-3x-15\le0\Leftrightarrow x\le-5\)

\(c2:3x+5x^2\ge-6+5x+5x^2\Leftrightarrow2x-6\le0\Leftrightarrow x\le3\)
\(c3:-x+7=6a-1\Leftrightarrow x=-\left(6a-1-7\right)=8-6a>0\Leftrightarrow a< \dfrac{4}{3}\)
\(c4:pt\Leftrightarrow\left(2019-x\right)^3+\left(2021-x\right)^3+\left[2x-4040\right]^3=0\left(1\right)\)
\(đặt:\left[\left(2019-x\right);\left(2021-x\right)\right]=\left\{u;v\right\}\)
\(\Rightarrow2x-4040=x-2019+x-2021=-u-v\)
\(\left(1\right)\Leftrightarrow u^3+v^3+\left(-u-v\right)^3=0\Leftrightarrow-3uv\left(u+v\right)=0\Leftrightarrow\left[{}\begin{matrix}u.v=0\\u=-v\end{matrix}\right.\)
\(u.v=0\Leftrightarrow\left[{}\begin{matrix}u=0\Leftrightarrow2019-x=0\Leftrightarrow x=2019\\v=0\Leftrightarrow2021-x=0\Leftrightarrow x=2021\end{matrix}\right.\)
\(u=-v\Leftrightarrow2019-x=x-2021\Leftrightarrow x=2020\)
\(\Rightarrow S=\left\{2019;2020;2021\right\}\)
Câu 2 :
\(\Leftrightarrow3x+5x^2+6-5x-5x^2\ge0\Leftrightarrow-2x+6\ge0\Leftrightarrow x\le3\)
Câu 4 :
PT <=> \(2019-x+2021-x+2x-4040=0\Leftrightarrow2019+2021-4040=0\)
( đúng )
Vậy pt có vô số nghiệm


Gọi quãng đường AB là x (x>0)
Vận tốc xe máy đi từ A đến B là \(\dfrac{x}{30}\)
Vận tốc xe máy lúc về là \(\dfrac{x}{35}\)
Theo đề bài, ta có:
\(\dfrac{x}{30}-\dfrac{x}{35}=\dfrac{1}{3}\)
\(\Leftrightarrow\dfrac{7x-6x}{210}=\dfrac{70}{210}\)
\(\Leftrightarrow x=70\left(km\right)\left(tm\right)\)
Vậy quãng đường AB là 70km

a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12






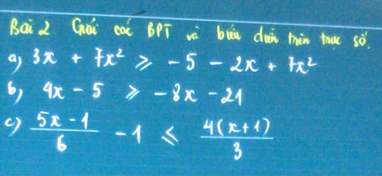




Gọi quãng đường AB là x ( x > 0 )
Theo bài ra ta có pt \(\dfrac{x}{60}-\dfrac{x}{65}=\dfrac{12}{60}=\dfrac{1}{5}\Rightarrow x=156\left(tm\right)\)
Vậy ...
na ná á
Xét ΔABC có BD là phân giác
nên AB/AD=BC/CD
=>AB/4=BC/5
Đặt AB/4=BC/5=k
=>AB=4k; BC=5k
Theo đề, ta có: AB2+AC2=BC2AB2+AC2=BC2
⇔9k2=81⇔9k2=81
=>k=3
=>AB=12; BC=15