K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 9 2021
\(e,\left(x-2\right)^2-16=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\\ f,x^2-5x-14=0\\ \Leftrightarrow\left(x-7\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ g,8x\left(x-3\right)+x-3=0\\ \Leftrightarrow\left(8x+1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{8}\\x=3\end{matrix}\right.\)
11 tháng 12 2023
b: ĐKXĐ: x<>-3
\(\dfrac{3x+x^2}{x^2+x+1}\cdot\dfrac{3x^3-3}{x+3}\)
\(=\dfrac{x\left(x+3\right)}{x^2+x+1}\cdot\dfrac{3\left(x^3-1\right)}{x+3}\)
\(=\dfrac{3x\left(x-1\right)\left(x^2+x+1\right)}{x^2+x+1}=3x\left(x-1\right)\)
e: ĐKXĐ: \(x\notin\left\{4;-5\right\}\)
\(\dfrac{2x+10}{x^3-64}:\dfrac{\left(x+5\right)^2}{2x-8}\)
\(=\dfrac{2\left(x+5\right)}{\left(x-4\right)\left(x^2+4x+16\right)}\cdot\dfrac{2x-8}{\left(x+5\right)^2}\)
\(=\dfrac{2\cdot2\left(x-4\right)}{\left(x-4\right)\left(x^2+4x+16\right)}=\dfrac{4}{x^2+4x+16}\)
H9
HT.Phong (9A5)
CTVHS
30 tháng 6 2023
a) \(\left(2x+3\right)\left(4x^2-6x+9\right)-2\left(4x^3-1\right)\)
\(=\left(2x+3\right)\left[\left(2x\right)^2-2x\cdot3+3^2\right]-2\left(4x^3-1\right)\)
\(=\left[\left(2x\right)^3+3^3\right]-2\left(4x^3-1\right)\)
\(=\left(8x^3+27\right)-8x^3+2\)
\(=8x^3+27-8x^3+2\)
\(=29\)
Vậy: ....
c) \(2\left(x^3+y^3\right)-3\left(x^3+y^3\right)\)
\(=2\left(x+y\right)\left(x^2-xy+y^2\right)-3x^2-3y^2\)
\(=2\left(x^2-xy+y^2\right)\cdot1-3x^2-3y^2\)
\(=2x^2-2xy+2y^2-3x^2-3y^2\)
\(=-x^2-2xy-y^2\)
\(=-\left(x^2+2xy+y^2\right)\)
\(=-\left(x+y\right)^2\)
\(=-\left(1\right)^2=-1\)
Vậy: ...
KV
9 tháng 5 2023
Câu 9
a) 3(x - 2)(x + 2) < 3x² + x
⇔ 3(x² - 4) - 3x² - x < 0
⇔ 3x² - 12 - 3x² - x < 0
⇔ -x < 12
⇔ x > -12
Vậy S = {x | x > -12}
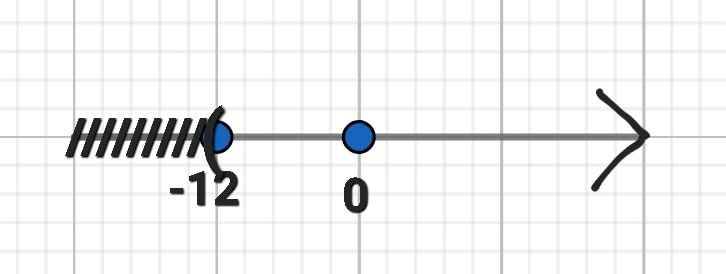
b) 6 + 2x ≥ 3 - x
⇔ 2x + x ≥ 3 - 6
⇔ 3x ≥ -3
⇔ x ≥ -1
Vậy S = {x | x ≥ -1}
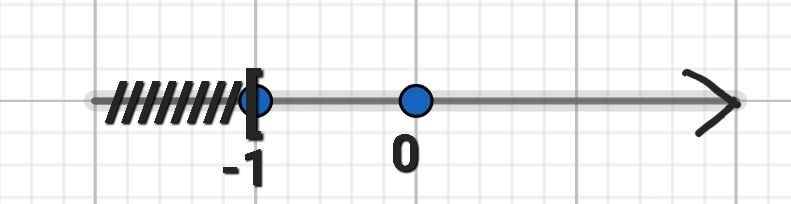
c) (x + 6)/4 - (x - 2)/6 < (x + 1)/3
⇔ 3(x + 6) - 2(x - 2) < 4(x + 1)
⇔ 3x + 18 - 2x + 4 < 4x + 4
⇔ 3x - 2x - 4x < 4 - 18 - 4
⇔ -3x < -18
⇔ x > 6
Vậy S = {x | x > 6}
14 tháng 10 2023
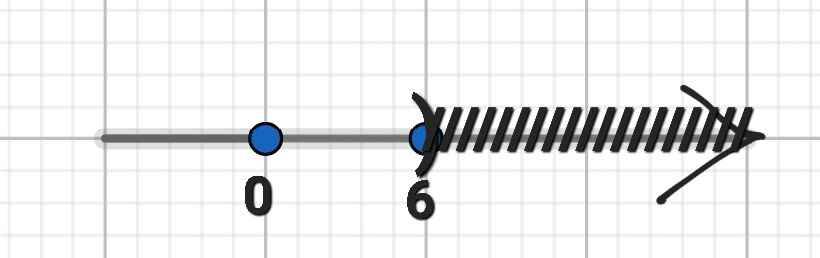
d) \(\dfrac{1}{x^4y^6z};\dfrac{2}{3x^2y^7z^2};\dfrac{3}{4x^5y}\)
Mẫu thức chung: \(12x^5y^7z^2\)
Quy đồng mẫu thức các phân thức ta được:
\(\dfrac{12xyz}{12x^5y^7z^2};\dfrac{8x^3}{12x^5y^7z^2};\dfrac{9y^6z^2}{12x^5y^7z^2}\)
AH
Akai Haruma
Giáo viên
15 tháng 7 2023
Lời giải:
a.
$-A=x^2-2x=(x^2-2x+1)-1=(x-1)^2-1\geq 0-1=-1$ (do $(x-1)^2\geq 0$ với mọi $x$)
$\Rightarrow A\leq 1$
Vậy $A_{\max}=1$. Giá trị này đạt tại $x=1$
b.
$-B=9x^2+6x-19=(9x^2+6x+1)-20=(3x+1)^2-20\geq 0-20=-20$
$\Rightarrow B\leq 20$
Vậy $B_{\max}=20$. Giá trị này đạt tại $3x+1=0\Leftrightarrow x=\frac{-1}{3}$
c.
$-C=3x^2-12x=3(x^2-4x)=3(x^2-4x+4)-12=3(x-2)^2-12\geq 3.0-12=-12$
$\Rightarrow C\leq 12$
Vậy $C_{\max}=12$. Giá trị này đạt tại $x-2=0\Leftrightarrow x=2$
d.
$-D=y^2-5y+4=(y^2-5y+2,5^2)-2,25=(y-2,5)^2-2,25\geq -2,25$
$\Rightarrow D\leq 2,25$
Vậy $D_{\max}=2,25$
Giá trị này đạt tại $y-2,5=0\Leftrightarrow y=2,5$
e.
$-E=3y^2-4y+7=3(y^2-\frac{4}{3}y)+7$
$=3[y^2-\frac{4}{3}y+(\frac{2}{3})^2]+\frac{17}{3}=3(y-\frac{2}{3})^2+\frac{17}{3}\geq \frac{17}{3}$
$\Rightarrow E\leq \frac{-17}{3}$
Vậy $E_{\max}=\frac{-17}{3}$ khi $y-\frac{2}{3}=0\Leftrightarrow y=\frac{2}{3}$
Y
13 tháng 6 2023
\(a,2x^3-6x^2-2x\left(x^2-3x+2\right)\)
\(=2x^3-6x^2-2x^3+6x^2-4x\)
\(=\left(2x^3-2x^3\right)+\left(-6x^2+6x^2\right)-4x\)
\(=0+0-4x\)
\(=-4x\)
\(b,-6x^2\left(3x-1\right)+2x\left(9x^2+5x\right)\)
\(=-18x^3+6x^2+18x^3+10x^2\)
\(=\left(-18x^3+18x^3\right)+\left(6x^2+10x^2\right)\)
\(=0+16x^2\)
\(=16x^2\)
13 tháng 6 2023
a. \(2x^3-6x^2-2x\left(x^2-3x+2\right)\\ =2x^3-6x^2-2x^3+6x^2-4x\\ =-4x\)
b. \(-6x^2\left(3x-1\right)+2x\left(9x^2+5x\right)\\ =-18x^3+6x^2+18x^3+10x^2\\ =6x^2+10x^2\\ =16x^2\)
17 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`b,`
\(B=x^6 - 20x^5 - 20x^4 - 20x^3 - 20x^2 - 20x + 3\) tại `x=21`
Ta có: `20 = 21 - 1 => 20 = x-1`
Thay `20 = x-1` vào, ta có:
\(x^6-\left(x-1\right)x^5-\left(x-1\right)x^4-\left(x-1\right)x^3-\left(x-1\right)x^2-\left(x-1\right)x+3\)
`=`\(x^6-x^6+x^5-x^5+x^4-x^4+...+x+3\)
`=`\(x+3\)
`=`\(21+3=24\)
Vậy, `B=24`
17 tháng 6 2023
`c,`
`C=`\(x^7-26x^6+27x^5-47x^4-77x^3+50x^2+x-24\) tại `x=25`
`=`\(x^7-25x^6-x^6+25x^5+2x^5-50x^4+3x^4-75x^3-2x^3+50x^2+x-24\)
`=`\(x^6\left(x-25\right)-x^5\left(x-25\right)+2x^4\left(x-25\right)+3x^3\left(x-25\right)-2x^2\left(x-25\right)+x-24\)
`=`\(\left(x^6-x^5+2x^4+3x^3-2x^2\right)\left(x-25\right)+x-24\)
Thay `x=25` vào bt C, ta được:
\(\left(25^6-25^5+2\cdot25^4+3\cdot25^3-2\cdot25^2\right)\left(25-25\right)+25-24\)
`=`\(\left(25^6-25^5+2\cdot25^4+3\cdot25^3-2\cdot25^2\right)\cdot0+1\)
`= 0+1=1`
Vậy, `C=1.`
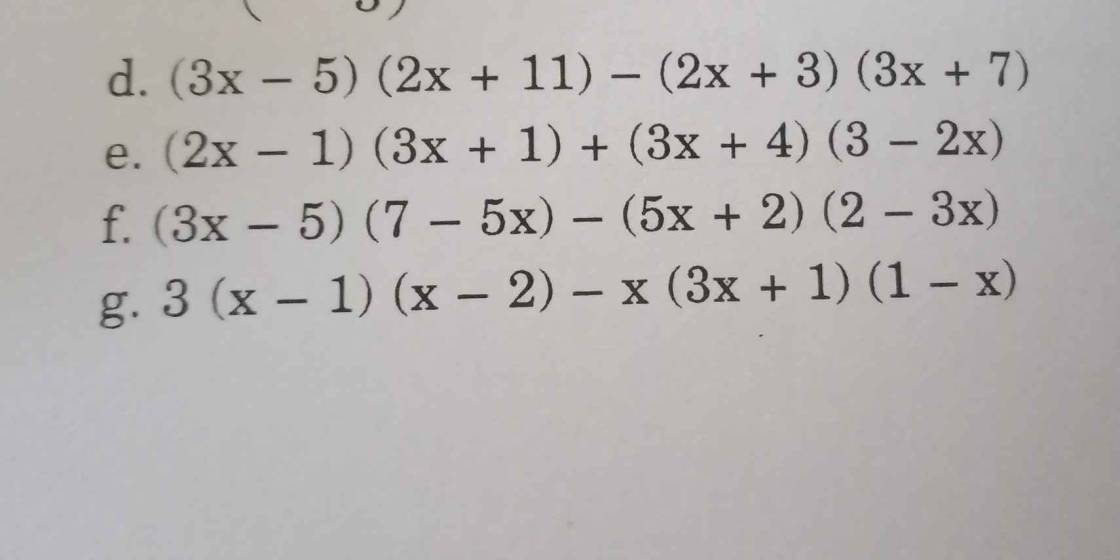
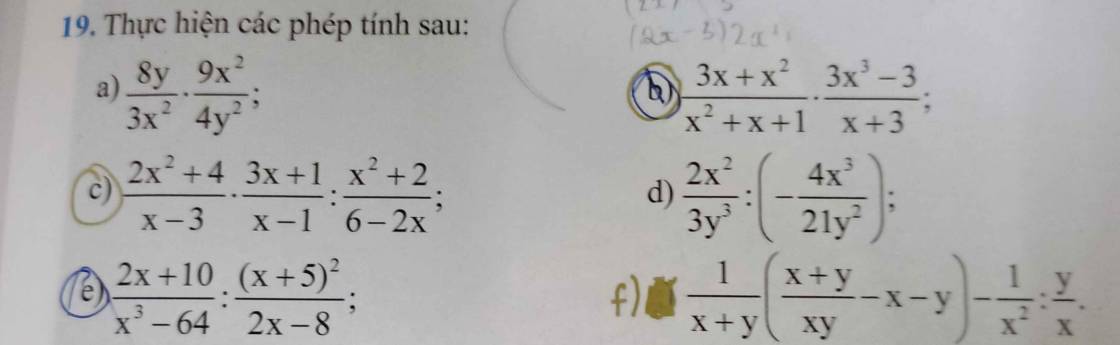
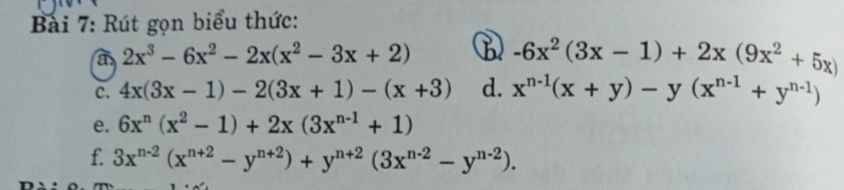
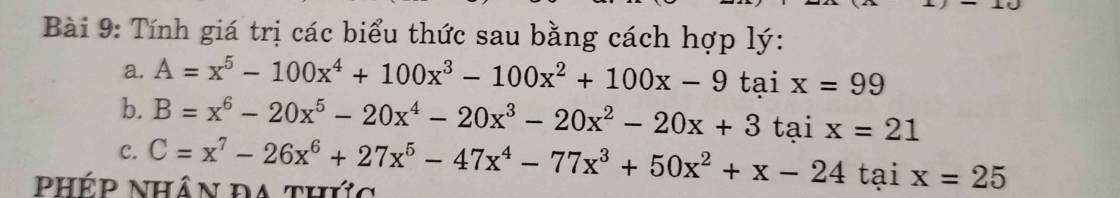
Đề yêu cầu gì em, thu gọn đa thức hả?
\(e,=6x^2-3x+2x-1+9x+12-6x^2-8x\\ =\left(6x^2-6x^2\right)+\left(-3x+2x+9x-8x\right)+\left(-1+12\right)\\ =11\\ g,=\left(3x-3\right)\left(x-2\right)-\left(3x^2+x\right)\left(1-x\right)\\ =3x^2-3x-6x+6-\left(3x^2+x-3x^3-x^2\right)\\ =3x^2-9x+6+3x^3-2x^2-x\\ =3x^3+x^2-10x+6\)