K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2022
4a.
\(y=2x^2-tanx\Rightarrow y'=\left(2x^2\right)'-\left(tanx\right)'=4x-\dfrac{1}{cos^2x}\)
b.
\(y'=\left(3tan\left(x+\dfrac{\pi}{3}\right)\right)'-\left(4sinx\right)'=3\left(x+\dfrac{\pi}{3}\right)'.\dfrac{1}{cos^2\left(x+\dfrac{\pi}{3}\right)}-4cosx\)
\(=\dfrac{3}{cos^2\left(x+\dfrac{\pi}{3}\right)}-4cosx\)
5a.
\(y'=\left(2x\right)'-\left(3sinx\right)'+\left(2cotx\right)'=2-3cosx-\dfrac{2}{sin^2x}\)
b.
\(y'=\left(cot\left(3x+\dfrac{\pi}{6}\right)\right)'-\left(4cosx\right)'=\left(3x+\dfrac{\pi}{6}\right)'.\dfrac{-1}{sin^2\left(3x+\dfrac{\pi}{6}\right)}+4sinx\)
\(=-\dfrac{3}{sin^2\left(3x+\dfrac{\pi}{6}\right)}+4sinx\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
a.
\(y'=\left(x^2\right)'+\left(4sinx\right)'=2x+4cosx\)
b.
\(y'=\left(2x^3\right)'-\left(sinx\right)'+\left(2\right)'=6x^2-cosx\)
c.
\(y'=\left(5sin\left(x-\dfrac{\pi}{4}\right)\right)'=5cos\left(x-\dfrac{\pi}{4}\right).\left(x-\dfrac{\pi}{4}\right)'=5cos\left(x-\dfrac{\pi}{4}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
a.
\(y=x^7\left(x+1\right)=x^8+x^7\)
\(\Rightarrow y'=8x^7+7x^6\)
b.
\(y'=2x+\dfrac{2}{2\sqrt{x}}=2x+\dfrac{1}{\sqrt{x}}\)
c.
\(y'=9x^2+4x\)
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
1.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=\left(-x^3-x\right)tan\left(-3x\right)=\left(x^3+x\right)tan3x=f\left(x\right)\)
Hàm chẵn
2.
\(D=R\)
\(f\left(-x\right)=\left(-2x+1\right)sin\left(-5x\right)=\left(2x-1\right)sin5x\ne\pm f\left(x\right)\)
Hàm không chẵn không lẻ
3.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=tan\left(-3x\right).sin\left(-5x\right)=-tan3x.\left(-sin5x\right)=tan3x.sin5x=f\left(x\right)\)
Hàm chẵn
4.
\(D=R\)
\(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-10x\right)=sin^22x+cos10x=f\left(x\right)\)
Hàm chẵn
5.
\(D=R\backslash\left\{k\pi\right\}\) là miền đối xứng
\(f\left(-x\right)=\dfrac{-x}{sin\left(-x\right)}=\dfrac{-x}{-sinx}=\dfrac{x}{sinx}=f\left(x\right)\)
Hàm chẵn
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
a.
Do chóp tứ giác đều \(\Rightarrow\Delta SAC\) cân tại A
Mà O là tâm đáy \(\Rightarrow O\) là trung điểm AC
\(\Rightarrow SO\perp AC\) (trung tuyến đồng thời là đường cao trong tam giác cân)
Hoàn toàn tương tự, ta có \(SO\perp BD\)
\(\Rightarrow SO\perp\left(ABCD\right)\)
b.
Ta có: \(AC\perp BD\) (hai đường chéo hình vuông)
Theo cmt, \(SO\perp AC\)
\(\left\{{}\begin{matrix}SO\in\left(SBD\right)\\BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\)
Tương tự: \(\left\{{}\begin{matrix}BD\perp AC\\BD\perp SO\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
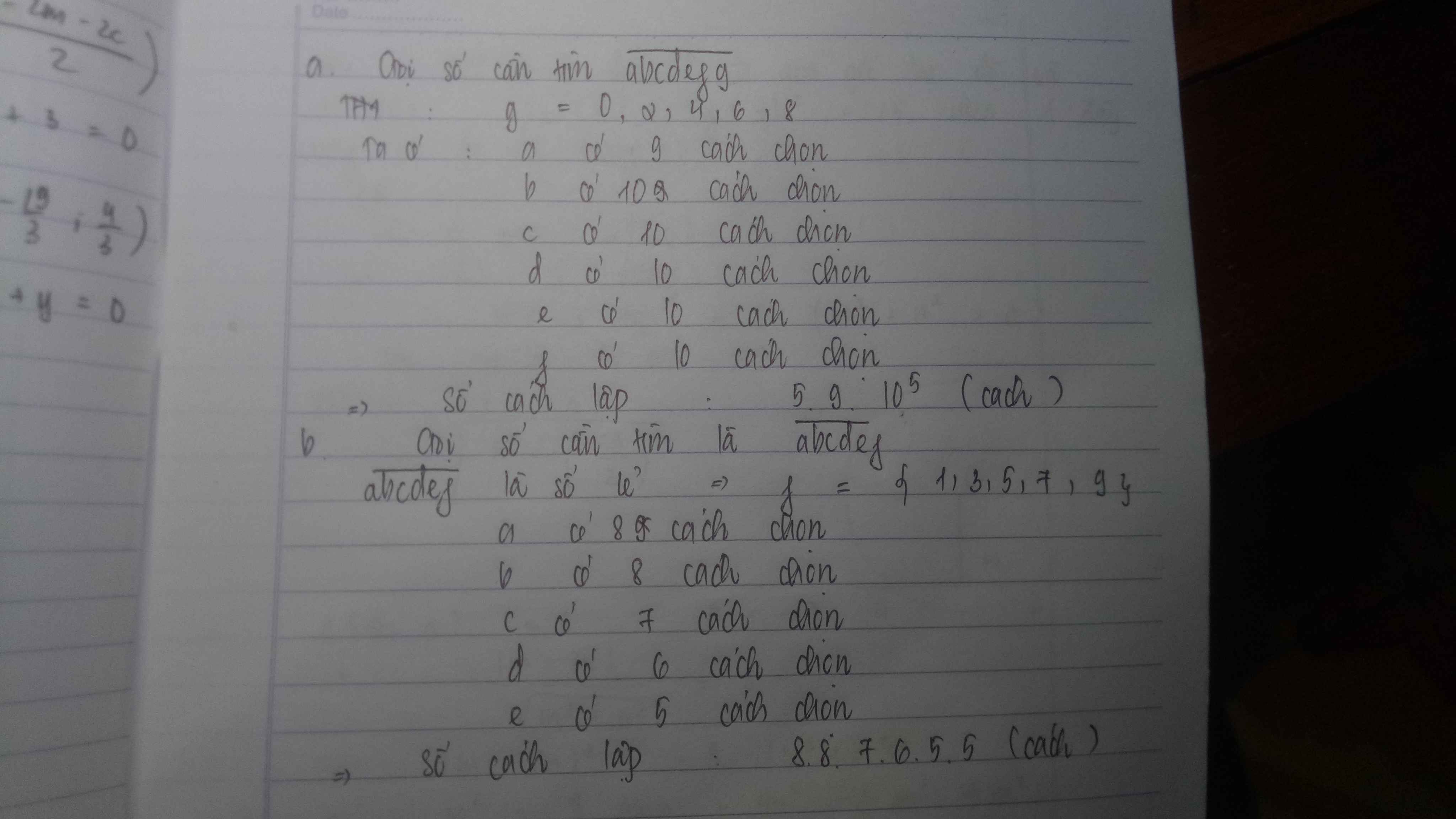
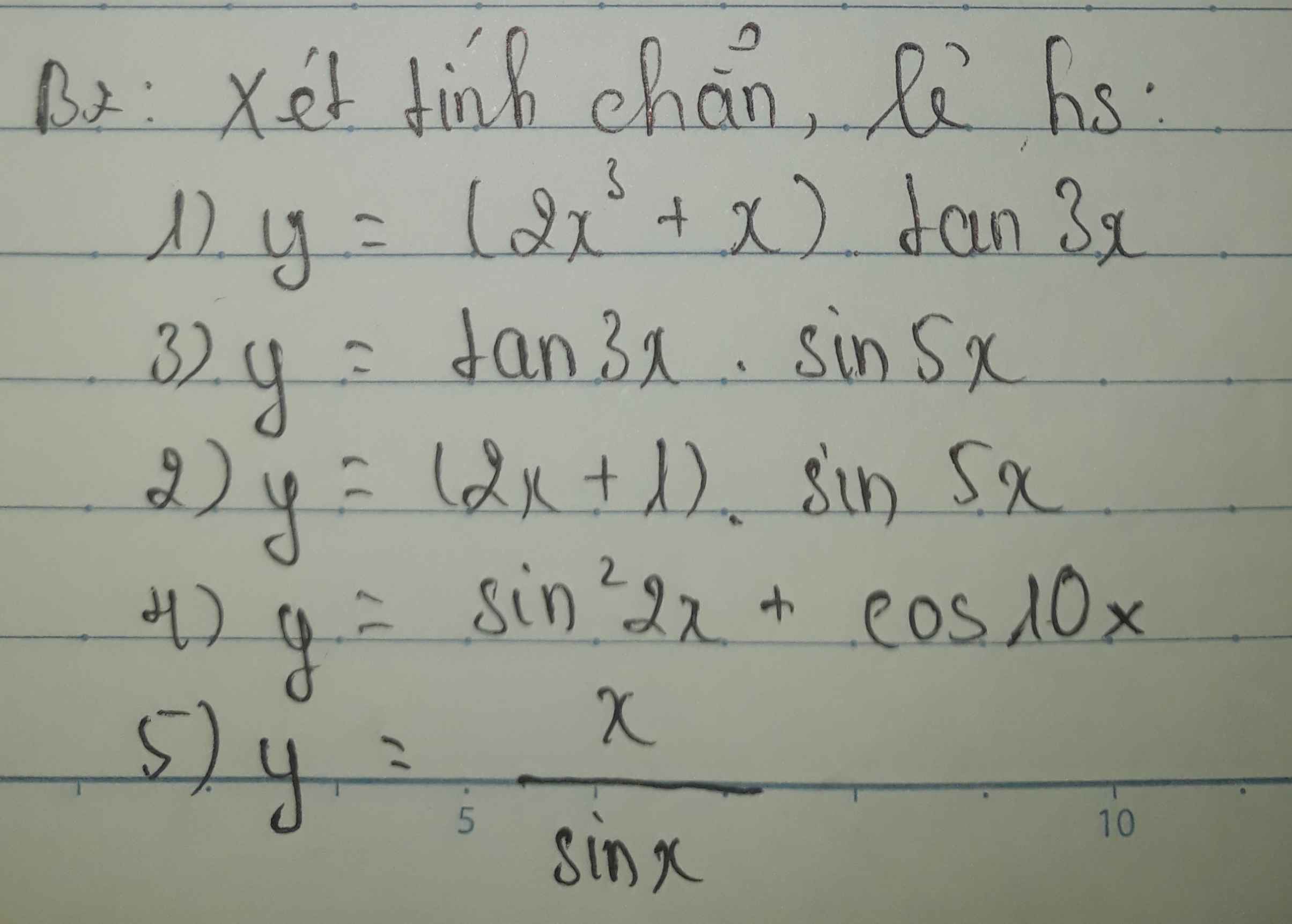
a.
\(y'=\left(x^2\right)'+\left(4sinx\right)'=2x+4cosx\)
b.
\(y'=\left(2x^3\right)'-\left(sinx\right)'+\left(2\right)'=6x^2-cosx\)
c.
\(y'=\left(5sin\left(x-\dfrac{\pi}{4}\right)\right)'=5.\left(x-\dfrac{\pi}{4}\right)'.cos\left(x-\dfrac{\pi}{4}\right)=5cos\left(x-\dfrac{\pi}{4}\right)\)