K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 10 2021
\(k,=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)+5\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}+5}\\ =\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}+5\right)}{\sqrt{a}+\sqrt{b}+5}=\sqrt{a}-\sqrt{b}\)
8 tháng 10 2021
\(h,=\dfrac{1}{2a-1}\sqrt{25a^2\left(a^2-4a+4\right)}=\dfrac{1}{2a-1}\sqrt{25a^2\left(a-2\right)^2}\\ =\dfrac{\left|5a\left(a-2\right)\right|}{2a-1}=\left[{}\begin{matrix}\dfrac{5a\left(a-2\right)}{2a-1}\left(a\ge2;a\ne\dfrac{1}{2}\right)\\\dfrac{5a\left(2-a\right)}{2a-1}\left(0\le a< 2;a\ne\dfrac{1}{2}\right)\\\dfrac{-5a\left(2-a\right)}{2a-1}\left(a< 0\right)\end{matrix}\right.\)
19 tháng 8 2021
a: Ta có: \(\sqrt{75}-\sqrt{5\dfrac{1}{3}}+\dfrac{9}{2}\sqrt{2\dfrac{2}{3}}+2\sqrt{27}\)
\(=5\sqrt{3}+\dfrac{4}{3}\sqrt{3}+3\sqrt{6}+6\sqrt{3}\)
\(=\dfrac{37}{3}\sqrt{3}+3\sqrt{6}\)
c: Ta có: \(\left(\sqrt{12}+2\sqrt{27}\right)\cdot\dfrac{\sqrt{3}}{2}-\sqrt{150}\)
\(=\left(2\sqrt{3}+6\sqrt{3}\right)\cdot\dfrac{\sqrt{3}}{2}-5\sqrt{6}\)
\(=12-5\sqrt{6}\)
16 tháng 7 2021
Bài 2:
d) Ta có: \(\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}\)
\(=\sqrt{5}+1+\sqrt{5}-1\)
\(=2\sqrt{5}\)
e) Ta có: \(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)
24 tháng 9 2021
\(e,=\dfrac{\left(3+\sqrt{2}\right)\left(2\sqrt{2}+1\right)}{7}-\sqrt{\dfrac{\left(\sqrt{2}+1\right)^2}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}}\\ =\dfrac{7\sqrt{2}+7}{7}-\dfrac{\sqrt{2}+1}{1}=\sqrt{2}+1-\sqrt{2}-1=0\)
\(f,=\sqrt{\dfrac{\left(2\sqrt{3}-3\right)^2}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}}\left(2+\sqrt{3}\right)\\ =\dfrac{\left(2\sqrt{3}-3\right)\left(2+\sqrt{3}\right)}{\sqrt{3}}\\ =\dfrac{\sqrt{3}}{\sqrt{3}}=1\)
\(h,=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{20-9}}\left(\sqrt{2}+\sqrt{10}\right)\\ =\sqrt{\dfrac{2\left(33-11\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{\dfrac{22\left(3-\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{6-2\sqrt{5}}\left(\sqrt{5}+1\right)=\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)=4\)
NT
8 tháng 8 2021
\(E=\sqrt{12-6\sqrt{3}}+\sqrt{21-12\sqrt{3}}\)
\(=\sqrt{9-2.3\sqrt{3}+3}+\sqrt{12-2.3.2\sqrt{3}+9}\)
\(=\sqrt{\left(9-3\right)^2}+\sqrt{\left(12-9\right)^2}\)
\(=\sqrt{6^2}+\sqrt{3^2}\)
\(=6+3=9\)
8 tháng 8 2021
e) Ta có: \(E=\sqrt{12-6\sqrt{3}}+\sqrt{21-12\sqrt{3}}\)
\(=3-\sqrt{3}+2\sqrt{3}-3\)
\(=\sqrt{3}\)
f) Ta có: \(F=\sqrt{21-12\sqrt{3}}+\sqrt{21+12\sqrt{3}}\)
\(=2\sqrt{3}-3+2\sqrt{3}+3\)
\(=4\sqrt{3}\)
h) Ta có: \(H=\sqrt{14+6\sqrt{5}}+\sqrt{14-6\sqrt{5}}\)
\(=3+\sqrt{5}+3-\sqrt{5}\)
=6
17 tháng 8 2021
e: Ta có: \(E=\sqrt{19+8\sqrt{3}}-\sqrt{28-6\sqrt{3}}+\sqrt{12}\)
\(=4+\sqrt{3}-3\sqrt{3}+1+2\sqrt{3}\)
=5
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 8 2021
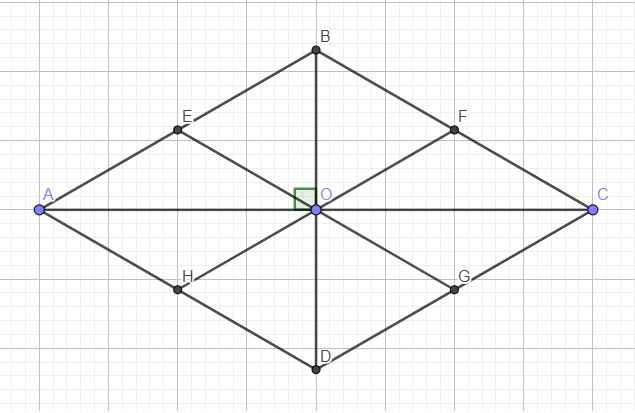
Do ABCD là hình thoi \(\Rightarrow\Delta BCD\) cân tại C
Mà \(C=60^0\Rightarrow\Delta BCD\) đều
Hoàn toàn tương tự, ta có tam giác ABD đều
\(\Rightarrow AB=BC=CD=DA=BD\) (1)
Gọi O là giao điểm 2 đường chéo \(\Rightarrow OA\perp OB\)
Trong tam giác vuông OAB, do E là trung điểm AB nên OE là trung tuyến ứng với cạnh huyền
\(\Rightarrow OE=\dfrac{1}{2}AB\) (2)
Mà O là trung điểm BD (tính chất hình thoi) \(\Rightarrow OB=\dfrac{1}{2}BD\) (3)
(1);(2);(3) \(\Rightarrow OE=OB\)
Hoàn toàn tương tự, ta có:
\(OE=OB=OF=OG=OD=OH\)
\(\Rightarrow\) Các điểm E, B, F, G, D, H cùng thuộc 1 đường tròn tâm O bán kính OB
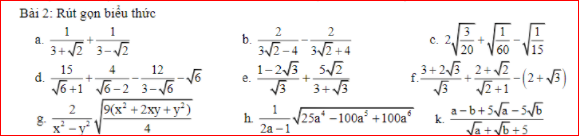
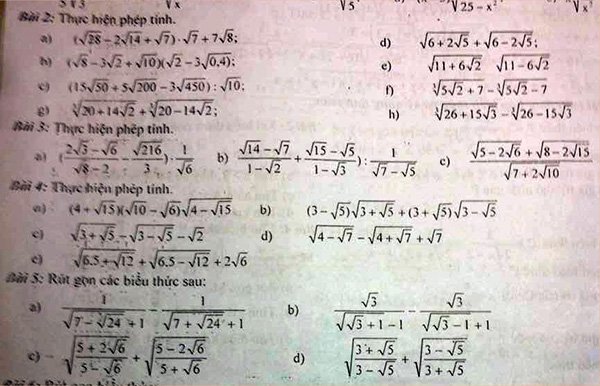
\(2,\\ a,x=36\Leftrightarrow P=\dfrac{6+1}{6-2}=\dfrac{7}{4}\\ b,x=6-2\sqrt{5}\Leftrightarrow\sqrt{x}=\sqrt{5}-1\\ \Leftrightarrow P=\dfrac{\sqrt{5}-1+1}{\sqrt{5}-1-2}=\dfrac{\sqrt{5}}{\sqrt{5}-3}=\dfrac{5-3\sqrt{5}}{2}\\ c,x=\dfrac{2}{2+\sqrt{3}}=4-2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{3}-1\\ \Leftrightarrow P=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-2}=\dfrac{\sqrt{3}}{\sqrt{3}-3}=\dfrac{3\left(\sqrt{3}+1\right)}{-6}=\dfrac{-\sqrt{3}-1}{2}\)
giúp mk câu d,e,f,g,h bn ơi