
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a. \(=2\sqrt{3^2}+\sqrt{15}-\sqrt{4.15}=6+\sqrt{15}-2\sqrt{15}=6-\sqrt{15}\)
b. \(=5\sqrt{10}+2\sqrt{5^2}-\sqrt{25.10}=5\sqrt{10}+10-5\sqrt{10}=10\)
c. \(=\left(\sqrt{4.7}-\sqrt{4.3}-\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\)
\(=2\sqrt{7^2}-2\sqrt{21}-\sqrt{7^2}+2\sqrt{21}=7\)
d. \(=\left(\sqrt{9.11}-\sqrt{9.2}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)
\(=\left(3\sqrt{11}-3\sqrt{2}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)
\(=3\sqrt{11^2}-3\sqrt{22}-\sqrt{11^2}+3\sqrt{22}=22\)
Bài 3:
a.
\(=\left(1-\sqrt{x}\right)\left(1+\sqrt{x}+\sqrt{x}^2\right)=1-\sqrt{x}^3=1-x\sqrt{x}\)
b.
\(=\left(\sqrt{x}+2\right)\left(\sqrt{x}^2-2\sqrt{x}+2^2\right)=\sqrt{x}^3+2^3=x\sqrt{x}+8\)
c.
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}^2+\sqrt{xy}+\sqrt{y}^2\right)=x\sqrt{x}-y\sqrt{y}\)
d.
\(=\left(x+\sqrt{y}\right)\left(x^2-x\sqrt{y}+\sqrt{y}^2\right)=x^3+y\sqrt{y}\)


12:
a: góc MHD+góc MED=180 độ
=>MHDE nội tiếp
b: Xét ΔDHC vuông tại H và ΔDEB vuông tại E có
góc HDC=góc EDB
=>ΔDHC đồng dạng với ΔDEB
=>DH/DE=DC/DB
=>DH*DB=DE*DC
c: Xét ΔDCB có
BH,CE là đừog cao
BH cắt CE tại D
=>D là trực tâm
=>MD vuông góc CB
=>MD//AC
mà AM//CD
nên AMDC là hình bình hành
=>H là trung điểm của AD

a: \(\dfrac{1}{\sqrt{n}}=\dfrac{2}{\sqrt{n}+\sqrt{n}}< \dfrac{2}{\sqrt{n}+\sqrt{n-1}}\)
\(=2\left(\sqrt{n}-\sqrt{n-1}\right)\)
\(\dfrac{1}{\sqrt{n}}=\dfrac{2}{\sqrt{n}+\sqrt{n}}>\dfrac{2}{\sqrt{n}+\sqrt{n+1}}=2\left(\sqrt{n+1}-\sqrt{n}\right)\)
=>\(2\left(\sqrt{n+1}-\sqrt{n}\right)< \dfrac{1}{\sqrt{n}}< 2\left(\sqrt{n}-\sqrt{n-1}\right)\)
b: 2(căn 101-căn 2)<1/căn 2+1/căn 3+...+1/căn 100<2(căn 100-căn 1)=18
2(căn 101-căn 2)=2căn 101-2căn 2>2căn 100-3=17
=>\(17< \dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{100}}< 18\)

4:
Gọi chiều rộng là x
=>Chiều dài là x+3
Theo đề, ta có: x(x+3)=180
=>x^2+3x-180=0
=>(x+15)(x-12)=0
=>x=-15(loại) hoặc x=12(nhận)
=>Chiều dài là 15cm

a) nhân dạng liên hiệp
<=> \(\dfrac{4\left(\sqrt{7}+3\right)}{2}-\dfrac{3\left(\sqrt{7}+2\right)}{3}\)
= 2\(\sqrt{7}+6-\sqrt{7}-2\) = \(\sqrt{7}+4\)
b) (\(\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}+1}-\sqrt{x}\)).\(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
<=> ( x - \(\sqrt{x}+1-\sqrt{x}\) ) . \(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
<=> \(\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}\)= \(\dfrac{\sqrt{x}-1}{\sqrt{x}}\)

Đề bài đúng : Cho a,b,c là các số thoả mãn : \(a^2+b^2+c^2\le8\) Tìm giá trị nhỏ nhất của
Ta có : \(0\le\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ac\right)\)\(\Rightarrow ab+bc+ac\ge\frac{-\left(a^2+b^2+c^2\right)}{2}\ge-4\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}a^2+b^2+c^2=8\\a+b+c=0\end{cases}}\)
Mặt khác : \(\frac{a^2+b^2}{2}\ge-ac\Rightarrow ac\ge\frac{-\left(a^2+b^2\right)}{2}\ge\frac{-\left(a^2+b^2+c^2\right)}{2}\ge-4\)
\(\Rightarrow ab+bc+2ac\ge-4-4=-8\)
Min \(ab+bc+2ac=-8\Leftrightarrow a=2,b=0,c=-2\)




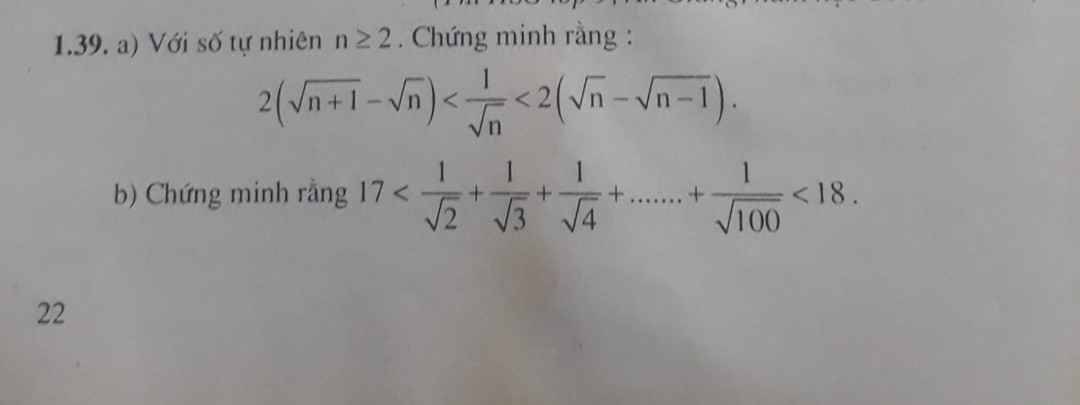

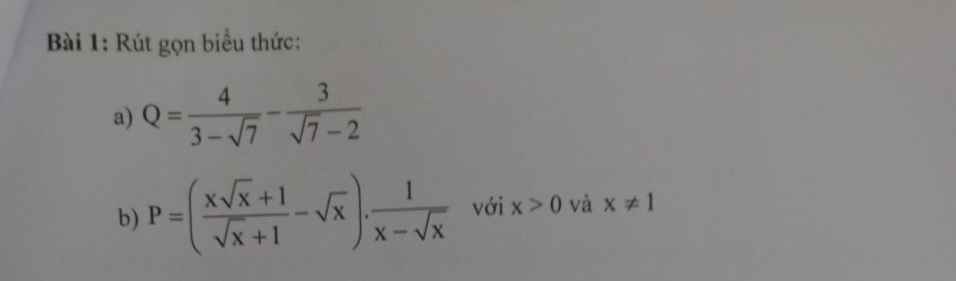
`12)`
`a)` Căn thức có nghĩa `<=>-2x+3 >= 0<=>-2x >= -3<=>x <= 3/2`
`b)` Căn thức có nghĩa `<=>{(2/[x^2] >= 0),(x^2 ne 0):}<=>x ne 0`
`c)` Căn thức có nghĩa `<=>4/[x+3] >= 0<=>x+3 > 0<=>x > -3`
`d)` Căn thức có nghĩa `<=>[-5]/[x^2+6] >= 0`
Vì `-5 < 0` mà `x^2+6 > 0`
`=>[-5]/[x^2+6] < 0 AA x`
`=>` Không có giá trị `x` nào để căn thức có nghĩa.
cảm ơn nhiêu ạ