Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây
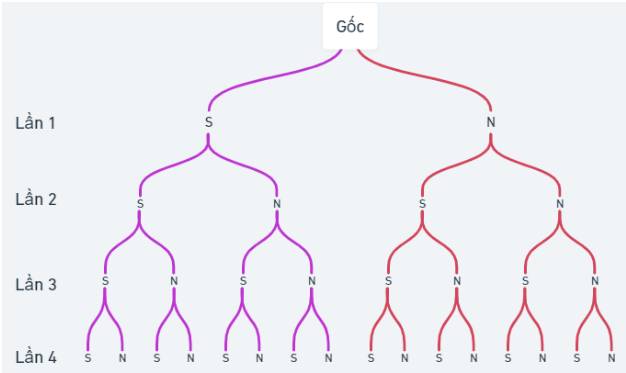
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”
Suy ra \(A = \left\{ {SSNN;SNSN;SNNS;NSSN;NSNS;NNSS} \right\}\). Suy ra \(n\left( A \right) = 6\). Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).

a: n(A)=2
n(omega)=2*2*2=8
=>P(A)=2/8=1/4
b: B={(NSS); (SNS); (SSN)}
=>n(B)=3
=>P(B)=3/8
c: C={NSS; NSN; SSN; SSS}
=>n(C)=4
=>P(C)=4/8=1/2
d: D={NSN; NNS; NNN; SNN; NSS; SNS; SSN}
=>n(D)=6
=>P(D)=6/8=3/4

Lời giải:
Mỗi lần gieo sẽ có 2 khả năng (sấp, ngửa). Gieo 4 lần sẽ có thể có $2^4=16$ khả năng xảy ra (không gian mẫu)
Các khả năng tung mà có ít nhất 2 lần xuất hiện mặt ngửa:
NNSS, NNSN, NNNN, NNNS, SNNN, SNNS, SSNN, NSNN
=> có 8 khả năng.
Xác suất: $\frac{8}{16}=\frac{1}{2}$

Câu 1: Gieo 1 đồng tiền cân đối và đồng chất 2 lần
\(\Rightarrow n\left(\Omega\right)=2^2=4\)
Gọi A là biến cố cả hai lần xuất hiện mặt sấp
\(\Rightarrow A=\left\{SS\right\}\Rightarrow n\left(A\right)=1\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{1}{4}\)
Chọn B
Câu 2: Số phần tử không gian mẫu: \(n\left(\Omega\right)=6\)
Gọi biến cố A: “Số chấm là số nguyên tố xuất hiện”
\(A=\left\{2;3;5\right\}\)
\(\Rightarrow n\left(A\right)=3\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{3}{6}=\dfrac{1}{2}\)
Chọn A

Gọi X là số lần mặt N xuất hiện trong 10000 lần gieo đó, ta có X là BBN nhị thức B(10000 ; 0,5). Xác suất cần tìm là P(5000 < X < 5100) vì n khá lớn nên :
\(P\left(5010< X< 5100\right)=\Phi\left(\frac{5100-10000.0,5}{\sqrt{10000.0,5.0,5}}\right)\)\(-\Phi\left(\frac{5050-5000}{\sqrt{2500}}\right)\)
\(=\Phi\left(2\right)-\Phi\left(2\right)=0,474-0,314\)
\(=0,16\)
Vậy xác suất để trong 10000 lần gieo đó số lần mặt N xuất hiện nằm trong khoảng (5050,5100) là 0,16

Tổng số kết quả có thể xảy ra của phép thử là \(n\left( \Omega \right) = {2^4}\)
a) Biến cố đối của biến cố “Xuất hiện ít nhất ba mặt sấp” là biến cố “ Xuất hiện nhiều nhất một mặt sấp”
Biến cố xảy ra khi trên mặt đồng xu chỉ xuất hiện một hoặc không có mặt sấp nào. Số kết quả thuận lợi cho biến cố là \(C_4^1 + 1 = 5\)
Xác suất của biến cố là \(P = \frac{5}{{{2^4}}} = \frac{5}{{16}}\)
b) Biến cố đối của biến cố “Xuất hiện ít nhất một mặt ngửa” là biến cố “ Không xuất hiện mặt ngửa nào”
Biến cố xảy ra khi tất cả các mặt đồng là mặt sấp. Chỉ có 1 kết quả thuận lợi cho biến cố
Xác suất của biến cố là \(P = \frac{1}{{{2^4}}} = \frac{1}{{16}}\)

Sửa đề: Xuất hiện mặt 2 chấm
n(A)=1
n(omega)=6
=>P(A)=1/6

\(\Omega=\left\{\left(i\right)|i=1,2,3,4,5,6\right\}\)
\(\Rightarrow n\left(\Omega\right)=6\)
Gọi \(A:``\) Xuất hiện trên hai mặt chấm\("\)
\(A=\left\{3,4,5,6\right\}\)
\(\Rightarrow n\left(A\right)=4\)
\(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{4}{6}=\dfrac{2}{3}\)
Không gian mẫu: Ω= {1;2;3;4;5;6} →n(Ω)=6
Gọi biến cố A:" Xuất hiện trên hai mặt chấm"
A ={3;4;5;6} ➝n(A)= 4
Do đó, p(A)=\(\dfrac{n\left(A\right)}{n\left(\Omega\right)}\)=\(\dfrac{4}{6}\)=\(\dfrac{2}{3}\)

Mỗi lần gieo có 2 khả năng xảy ra: xấp hoặc ngửa
Nếu người đó gieo 3 lần thì có thể có số khả năng xảy ra là:
2.2.2 = 8 (khả năng)
n(omega)=2*2*2=8
A={(NNS); (NSN); (SNN)}
=>n(A)=3
=>P(A)=3/8