Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố thỏa mãn yêu cầu bài toán:
![]()
![]() nên n(A) = 8
nên n(A) = 8
Vậy ![]()

Gọi B là biến cố: “Tổng số chấm xuất hiện trên bề mặt con súc sắc bằng 12”
Ta thấy
12 = 1 + 5 + 6 = 2 + 4 + 6 = 2 + 5 + 5 = 3 + 3 + 6 = 3 + 4 + 5 = 4 + 4 + 4
Nếu số chấm trên bề mặt 3 con súc sắc khác nhau tức là các trường hợp (1;5;6), (2;4;6), (3;4;5) có 3 ! .3 = 18 cách
Nếu số chấm trên bề mặt 3 con súc sắc có 2 con giống nhau tức là các trường hợp (2;5;5) và (3;3;6) có 3.2 = 6 cách
Nếu số chấm trên bề mặt 3 con súc sắc giống nhau ta có 1 cách gieo duy nhất
⇒ n B = 18 + 6 + 1 = 25 . Vậy P B = n B Ω B = 25 216 .
Chọn A

Số phần tử của không gian mẫu là:
Ω = 6 3 = 216 .
A: “số chấm xuất hiện trên 3 con súc sắc đó bằng nhau”.
A = 1 , 1 , 1 ; 2 , 2 , 2 ; 3 , 3 , 3 ; 4 , 4 , 4 ; 5 , 5 , 5 ; 6 , 6 , 6
⇒ n A = 6
Xác suất để số chấm xuất hiện trên 3 con súc sắc đó bằng nhau là:
P = 6 216 = 1 36
Chọn đáp án D.

Đáp án là A.
• Số phần tử không gian mẫu n ( Ω ) = 36
• Gọi biến cố A: " Số chấm xuất hiện trên mặt của hai con súc sắc là số chẳn".
Ta có các khả năng xảy ra:
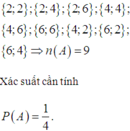

Số phần tử của không gian mẫu là: Ω = 6.6 = 36 .
Gọi biến cố A:”tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 7”.
Các kết quả thuận lợi cho A là:
A= { ( 1; 6) ; ( 2; 5); (3; 4); (4; 3); ( 5; 2); (6; 1)}.
Do đó, Ω A = 6 . Vậy P ( A ) = 6 36 = 1 6 .
Chọn đáp án B.

a: \(\Omega=\left\{\left(1;1\right);\left(1;2\right);\left(1;3\right);...;\left(6;5\right);\left(6;6\right)\right\}\)
b: A={(1;2); (2;1)}
=>P(A)=2/36=1/18
B={(4;1); (5;2); (6;3); (1;4); (2;5); (3;6)}
=>P(B)=6/36=1/6

Đáp án D
Tổng số chấm bẳng 2 khi số chấm ở 2 con xúc sắc là (1; 1).
Tổng số chấm bẳng 3 khi số chấm ở 2 con xúc sắc là (1; 2); (2; 1)
Tổng số chấm bẳng 4 khi số chấm ở 2 con xúc sắc là (1; 3); (2; 2); (3; 1)
Tổng số chấm bẳng 5 khi số chấm ở 2 con xúc sắc là (1; 4), (2; 3), (3; 2); (4; 1)
Do đó xác suất là 10 . 1 36 = 5 18