Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M( x; y) là giao điểm của 2 đường thẳng (a) và (b) ( nếu có).
Khi đó; tọa độ điểm M là nghiệm hệ phương trình:
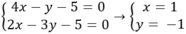
Vậy tọa độ giao điểm của 2 đường thẳng đã cho là : M( 1; -1)
Chọn C.

Thay tọa độ P, Q vào phương trình \(\Delta\) ta được 2 giá trị cùng dấu \(\Rightarrow\) P, Q nằm cùng phía so với \(\Delta\)
Gọi A là điểm đối xứng với \(P\) qua \(\Delta\Rightarrow AM=PM\)
\(\Rightarrow MP+MQ=AM+MQ\ge AQ\)
Dấu "=" xảy ra khi và chỉ khi A, M, Q thẳng hàng hay M là giao điểm AQ và \(\Delta\)
Phương trình đường thẳng d qua P và vuông góc \(\Delta\) có dạng:
\(1\left(x-1\right)+2\left(y-6\right)=0\Leftrightarrow x+2y-13=0\)
Tọa độ giao điểm H giữa d và \(\Delta\) là nghiệm: \(\left\{{}\begin{matrix}2x-y-1=0\\x+2y-13=0\end{matrix}\right.\) \(\Rightarrow H\left(3;5\right)\)
A đối xứng P qua \(\Delta\) khi và chỉ khi H là trung điểm AP \(\Rightarrow A\left(5;4\right)\)
\(\Rightarrow\overrightarrow{QA}=\left(8;8\right)=8\left(1;1\right)\Rightarrow\) đường thẳng AQ nhận (1;-1) là 1 vtpt
Phương trình AQ:
\(1\left(x+3\right)-1\left(y+4\right)=0\Leftrightarrow x-y-1=0\)
Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}x-y-1=0\\2x-y-1=0\end{matrix}\right.\) \(\Rightarrow M\left(0;-1\right)\)

Gọi M( x; y) là giao điểm của đường thẳng (d) và đường thẳng y= 2
Khi đó; tọa độ điểm M là nghiệm hệ phương trình:
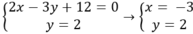
Vậy M( - 3; 2)
Chọn B.

Câu 1:
Ta dễ dàng kiểm tra được \(C\notin\left(d_1\right):2x-3y+12=0\) nên hai đường thẳng \(\left(d_1\right),\left(d_2\right)\) không là đường cao và trung tuyến kẻ từ \(C\).
Không mất tính tổng quát giả sử chúng kẻ từ \(A\)
\(\Rightarrow\left\{{}\begin{matrix}A\in\left(d_1\right)\\A\in\left(d_2\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x_A-3y_A+12=0\\2x_A+3y_A=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_A=-3\\y_A=2\end{matrix}\right.\Rightarrow A\left(-3;2\right)\)
Gọi trung điểm \(BC\) là \(M\) \(\Rightarrow M\in\left(d_2\right)\) \(\Rightarrow M\left(-\dfrac{3}{2}y;y\right)\)\(\Rightarrow\overrightarrow{CM}=\left(-\dfrac{3}{2}y-4;y-1\right)\).
VTPT của \(\left(d_1\right)\) là \(\overrightarrow{n}=\left(2;-3\right)\).
Do \(\left(d_1\right)\) vuông góc \(BC\) nên \(\overrightarrow{CM}=k\overrightarrow{n}\)
\(\Rightarrow\left\{{}\begin{matrix}-\dfrac{3}{2}y-4=2k\\y-1=-3k\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=-\dfrac{28}{5}\\k=\dfrac{11}{5}\end{matrix}\right.\Rightarrow M\left(\dfrac{42}{5};-\dfrac{28}{5}\right)\)
\(\Rightarrow B\left(\dfrac{64}{5};-\dfrac{61}{5}\right)\).
Câu 2:
\(\left\{{}\begin{matrix}B\in d_1\\B\in d_2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y-1=0\\2x+3y-6=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-3\\y=4\end{matrix}\right.\Rightarrow B\left(-3;4\right)\)
Gọi \(M\) là trung điểm \(AC\) \(\Rightarrow M\in d_2\Rightarrow M\left(x;2-\dfrac{2}{3}x\right)\Rightarrow\overrightarrow{AM}=\left(x-1;1-\dfrac{2}{3}x\right)\)
VTPT của \(d_1\) là \(\overrightarrow{n}=\left(1;1\right)\),
Do \(d_1\) vuông góc \(AC\Rightarrow\overrightarrow{AC}=k\overrightarrow{n}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=k\\1-\dfrac{2}{3}x=k\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{6}{5}\\k=\dfrac{1}{5}\end{matrix}\right.\Rightarrow M\left(\dfrac{6}{5};\dfrac{6}{5}\right)\)
\(\Rightarrow C\left(\dfrac{7}{5};\dfrac{7}{5}\right)\).

4 câu giống nhau, mình làm câu a, bạn tự làm 3 câu còn lại hoàn toàn tương tự:
a/ Đường thẳng d nhận \(\left(1;-2\right)\) là 1 vtpt
Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow\) d' nhận \(\left(2;1\right)\) là 1 vtpt
Phương trình d':
\(2\left(x-4\right)+1\left(y-1\right)=0\Leftrightarrow2x+y-9=0\)
Gọi H là hình chiếu vuông góc của M lên d \(\Rightarrow\) H là giao điểm của d và d'
Tọa độ H là nghiệm: \(\left\{{}\begin{matrix}x-2y+4=0\\2x+y-9=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{14}{5};\frac{17}{5}\right)\)
Gọi M' là điểm đối xứng với M qua d \(\Rightarrow\) H là trung điểm MM'
Tọa độ M': \(\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=\frac{8}{5}\\y_{M'}=2y_H-y_M=\frac{29}{5}\end{matrix}\right.\) \(\Rightarrow M'\left(\frac{8}{5};\frac{29}{5}\right)\)

a, Bán kính: \(R=2\sqrt{5}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=20\)
Giao điểm của d và (C) có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}\left(x+1\right)^2+\left(y-2\right)^2=20\\x+3y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3y+4\right)^2+\left(y-2\right)^2=20\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10y^2+20y=0\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x=-5\end{matrix}\right.\\\left\{{}\begin{matrix}y=-2\\x=1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}M=\left(0;-5\right)\\N=\left(-2;1\right)\end{matrix}\right.\) là các giao điểm
b, Gọi H là trung điểm AB.
Đường thẳng \(\Delta\) vuông góc với d nên có phương trình dạng: \(3x-y+m=0\left(m\in R\right)\)
Ta có: \(S_{IAB}=\dfrac{1}{2}.R^2.sinAIB=10.sinAIB=5\sqrt{3}\)
\(\Rightarrow sinAIB=\dfrac{\sqrt{3}}{2}\)
Mà tam giác ABC tù nên \(\widehat{AIB}=120^o\)
\(\Rightarrow\widehat{HBI}=30^o\)
Khi đó:
\(IH=d\left(I;\Delta\right)\)
\(\Leftrightarrow R.sinHBI=\dfrac{\left|-3-2+m\right|}{\sqrt{10}}\)
\(\Leftrightarrow2\sqrt{5}.sin30^o=\dfrac{\left|m-5\right|}{\sqrt{10}}\)
\(\Leftrightarrow m=5\pm5\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:3x-y+5+5\sqrt{2}=0\\\Delta:3x-y+5-5\sqrt{2}=0\end{matrix}\right.\)
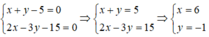
Chọn A.
Tọa độ giao điểm của hai đường thẳng x + y - 5 = 0 và 2x - 3y + 5 = 0 là nghiệm của hệ phương trình: