K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 2 2016
1+1=2 bởi vì coi 1 là một người đứng ở điểm A bước lên một bước là công thêm 1 đơn vị còn nếu lùi xuống 1 bước có nghĩa là bớt đi 1 đơn vị
=>1+1=2.
C2:coi 1 là a
coi 1 nữa là b
Ta có:
- (a-b)^2=0
(a^2)-2ab+b^2=0
a^2+b^2=2ab
mà a=1, b=1. Ghép vào biểu thức trên.
1^2+1^2=2x1x1
1+1=2.
Đó chính là lý do 1+1=2.
KV
6 tháng 6 2023
ĐKXĐ: x ≥ 0
Do x ≥ 0 ⇒ √x ≥ 0 và √x + 1 > 0
⇒ 0 ≤ √x < √x + 1
⇒ √x/(√x + 1) < 1
AE
3
7 tháng 6 2023
\(Xét:\dfrac{\sqrt{x}}{\sqrt{x}+1}\) ta thấy rõ ràng : \(\sqrt{x}\ge0\)
\(\Rightarrow\sqrt{x}+1\ge1\)
\(\Rightarrow\sqrt{x}\) không thể : \(\ge\sqrt{x}+1\)
Do đó : \(0< \dfrac{\sqrt{x}}{\sqrt{x}+1}< 1\)
DT
Dang Tung
CTVHS
7 tháng 6 2023
\(\dfrac{\sqrt{x}}{\sqrt{x}+1}\left(ĐK:x\ge0\right)\\ =\dfrac{\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\\ =1-\dfrac{1}{\sqrt{x}+1}\)
Ta thấy :
\(1>0,\sqrt{x}+1\ge1>0\forall x\ge0\\ =>\dfrac{1}{\sqrt{x}+1}>0\\ =>-\dfrac{1}{\sqrt{x}+1}< 0\\ =>1-\dfrac{1}{\sqrt{x}+1}< 1\\ =>\dfrac{\sqrt{x}}{\sqrt{x}+1}< 1\)
PT
1
CM
11 tháng 2 2019
3 x = 6 x - 3 y = 2 ⇔ x = 2 y = 1 3 x - 2 3
Ta có đường thẳng x = 2 song song với trục tung. Đường thẳng y = 1 3 x - 2 3 cắt trục tung nên hai đường thẳng đó cắt nhau. Hệ phương trình có 1 nghiệm duy nhất.
PT
1
CM
10 tháng 2 2018
(II):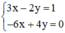 
Xét: (d): 3x – 2y = 1 hay (d):
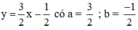
(d’): -6x + 4y = 0 hay (d’):
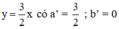
Ta có: a = a’ ; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ (II) vô nghiệm.
PT
1
CM
24 tháng 11 2019
3 x = 6 2 y = - 7
Đường thẳng 3x = 6 song song với trục tung. Đường thẳng 2y = -7 cắt trục tung nên hai đường thẳng đó cắt nhau. Hệ phương trình có 1 nghiệm duy nhất
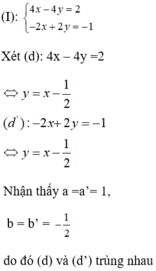
Vì khi ta làm đúng bài toán.
ví dụ có 1 quả táo thêm 1 quả nữa thì sẽ có 2 quả táo =>1 quả táo + 1 quả táo=2 quả táo
=>1+1=2