K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2019
Câu 1:
\(f\left(x\right)=\sqrt{\left(x+\frac{1}{2}\right)^2+\frac{3}{4}}-\sqrt{\left(x-\frac{1}{2}\right)^2+\frac{3}{4}}=m\)
Tọa độ hóa bài toán bằng cách gọi \(A\left(-\frac{1}{2};\frac{\sqrt{3}}{2}\right)\) và \(B\left(\frac{1}{2};\frac{\sqrt{3}}{2}\right)\) là hai điểm cố định trên mặt phẳng tọa độ Oxy, M là điểm di động có tọa độ \(M\left(x;0\right)\)
\(\Rightarrow AM=\left|\overrightarrow{AM}\right|=\sqrt{\left(x+\frac{1}{2}\right)^2+\left(0-\frac{\sqrt{3}}{2}\right)^2}=\sqrt{\left(x+\frac{1}{2}\right)^2+\frac{3}{4}}\)
\(BM=\left|\overrightarrow{BM}\right|=\sqrt{\left(x-\frac{1}{2}\right)^2+\frac{3}{4}}\)
\(\Rightarrow f\left(x\right)=AM-BM\)
Mặt khác, theo BĐT tam giác ta luôn có
\(\left|AM-BM\right|< AB=\sqrt{\left(\frac{1}{2}+\frac{1}{2}\right)^2+\left(\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}\right)^2}=1\)
\(\Rightarrow\left|f\left(x\right)\right|< 1\Rightarrow\left|m\right|< 1\Rightarrow-1< m< 1\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2019
Câu 2:
ĐKXĐ: \(1\le x\le3\)
Đặt \(\sqrt{x-1}+\sqrt{3-x}=a\ge0\)
Áp dụng BĐT Bunhiacốpxki:
\(\Rightarrow a\le\sqrt{\left(1+1\right)\left(x-1+3-x\right)}=2\sqrt{2}\)
Mặt khác
\(a^2=x-1+3-x+2\sqrt{\left(x-1\right)\left(3-x\right)}=2+2\sqrt{\left(x-1\right)\left(3-x\right)}\ge2\)
\(\Rightarrow2\le a\le3\)
Cũng từ trên ta có:
\(a^2=2+2\sqrt{\left(x-1\right)\left(3-x\right)}\Rightarrow\sqrt{\left(x-1\right)\left(3-x\right)}=\frac{a^2-2}{2}=\frac{1}{2}a^2-1\)
Phương trình trở thành:
\(a-\left(\frac{1}{2}a^2-1\right)=m\)
\(\Leftrightarrow-\frac{1}{2}a^2+a+1=m\)
Xét hàm \(f\left(a\right)=-\frac{1}{2}a^2+a+1\) trên \(\left[2;2\sqrt{2}\right]\)
\(f'\left(a\right)=-a+1< 0\) \(\forall a\in\left[2;2\sqrt{2}\right]\)
\(\Rightarrow f\left(a\right)\) nghịch biến trên \(\left[2;2\sqrt{2}\right]\)
\(\Rightarrow f\left(2\sqrt{2}\right)\le f\left(a\right)\le f\left(2\right)\Rightarrow-3+2\sqrt{2}\le f\left(a\right)\le1\)
Vậy:
- Nếu \(\left[{}\begin{matrix}m>1\\m< -3+2\sqrt{2}\end{matrix}\right.\) thì phương trình vô nghiệm
- Nếu \(-3+2\sqrt{2}\le m\le1\) pt có nghiệm
CM
15 tháng 3 2019
Đáp án D.
Tập xác định: D = R
y' = 3x2 – 3 => y’ = 0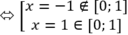 
y(0) = 1, y(1) = -1
Hàm số max[0;1]y = y(0) = 1
27 tháng 12 2021
\(PT\Leftrightarrow3^x+2^x-3x-2=0\left(1\right)\)
Ta thấy \(x=0;x=1\) là nghiệm của \(\left(1\right)\)
Xét hàm \(f\left(x\right)=3^x+2^x-3x-2,x\in R\\ f'\left(x\right)=3^x\ln3+2^x\ln2-3\\ f''\left(x\right)=3^x\ln^23+2^x\ln^22>0,\forall x\)
Bề lõm của \(f\left(x\right)\) luôn hướng về \(y>0\) nên đồ thị ko thể cắt trục hoành tại nhiều hơn 2 điểm
Vậy nghiệm PT là \(x=0;x=1\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 5 2021
Có thể nghịch suy để chọn hàm làm trắc nghiệm
Do \(x_2=\dfrac{x_3-x_1}{2}=1\) nên hàm có dạng: \(y=a\left(x-1\right)^4-b\left(x-1\right)^2+c\) với a;b;c dương
\(y'=0\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=\dfrac{b}{2a}\end{matrix}\right.\) \(\Rightarrow x_1;x_3\) thỏa mãn \(\left(x-1\right)^2=\dfrac{b}{2a}\) và \(f\left(x_2\right)=c\)
\(f\left(x_1\right)+f\left(x_3\right)+\dfrac{2}{3}f\left(x_2\right)=0\Leftrightarrow2f\left(x_1\right)+\dfrac{2}{3}f\left(x_2\right)=0\)
\(\Leftrightarrow a.\left(\dfrac{b}{2a}\right)^2-b\left(\dfrac{b}{2a}\right)+c+\dfrac{c}{3}=0\Rightarrow-\dfrac{b^2}{4a}+\dfrac{4c}{3}=0\)
Tới đây chọn \(a=3;c=1;b=4\) được hàm \(f\left(x\right)=3\left(x-1\right)^4-4\left(x-1\right)^2+1\)
Dễ dàng tính ra \(x_3=1+\sqrt{\dfrac{2}{3}}\) ; \(x_0=1+\sqrt{\dfrac{1}{3}}\) (với \(x_0\) là giao bên phải của đồ thị và trục hoành); \(f\left(x_1\right)=f\left(x_3\right)=-\dfrac{1}{3}\)
\(S_1+S_2=\int\limits^{x_0}_1f\left(x\right)dx-\int\limits^{x_3}_{x_0}f\left(x\right)dx\approx0,41\)
\(\dfrac{S_1+S_2}{S_3+S_4}=\dfrac{0,41}{\left(1+\dfrac{1}{3}\right)\left(x_3-1\right)-0,41}\approx0,6\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(\Leftrightarrow2^{-3}.2^{2x}-3.2^{-2}.2^x+1=0\)
\(\Leftrightarrow\dfrac{1}{8}2^{2x}-\dfrac{3}{4}2^x+1=0\)
Đặt \(2^x=t>0\)
\(\Rightarrow\dfrac{1}{8}t^2-\dfrac{3}{4}t+1=0\Rightarrow\left[{}\begin{matrix}t=4\\t=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2^x=4\\2^x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\)
NN
0
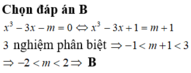
đặt pt là (*)
Gọi \(f\left(x\right)=x^3-3x+1\Rightarrow f\left(x\right)\)liên tục trên R
\(f\left(-2\right)=-1,f\left(0\right)=1\Rightarrow f\left(-2\right).f\left(0\right)< 0\Rightarrow\exists c_1\in\left(-2;0\right)\)là một nghiệm của (*)
\(f\left(0\right)=1,f\left(1\right)=-1\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow\exists c_2\in\left(0;1\right)\)là 1 nghiệm của (*)
\(f\left(1\right)=-1,f\left(2\right)=3\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow\exists c_3\in\left(1;2\right)\)là 1 nghiệm của (*)
dễ thấy \(c_1,c_2,c_3\)phân biệt nên pt(*) có 3 nghiệm phân biệt