VN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
3
LN
24 tháng 7 2017
=>\(\sqrt{\left(x+3\right)^2}\)+ \(\sqrt{\left(x+4\right)^2}\)+\(\sqrt{\left(x+5\right)^2}\)=9x
=> x + 3 + x + 4 + x + 5 = 9x
=> - 6x = - 12
=> x=2
25 tháng 7 2017
Ủa sao phá đc trị tuyệt đối hay v bạn? (căn a^2 = trị tuyệt đối của a )
LT
4
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
31 tháng 8 2015
\(\sqrt{\left(2x\right)^2+2.2x.5+5^2}+\sqrt{x^2+2.x.3+3^2}=10x-20\)
\(\Leftrightarrow\sqrt{\left(2x+5\right)^2}+\sqrt{\left(x+3\right)^2}=10x-20\)
\(\Leftrightarrow2x+5+x+3=10x-20\)
\(\Leftrightarrow7x=28\Leftrightarrow x=4\)
VT
10 tháng 9 2020
- giải phương trình sau:\(\sqrt{x^2+10x+26}+\sqrt{2x^2+20x+57}=1+\sqrt{7}\)bạn nào giải được mình bái phục bạn ấy à mình làm youtube nhé youtube của mình là: Long VH đăng ký nhé thanks
3 tháng 8 2017
a) giải pt ra ta được : x=-1
b) giải pt ra ta được : x=2
c)giải pt ra ta được : x vô ngiệm
d)giải pt ra ta được : x=vô ngiệm
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
DD
6 tháng 8 2015
\(\sqrt{x^2-10x+25}=7-2x=>\sqrt{\left(x-5\right)^2}=7-2x=>!x-5!=7-2x\)
\(x-5=7-2x\left(x>=5\right)=>3x=7+5=>x=4\)
\(5-x=7-2x\left(x2x-x=7-5=>x=2\)
HN
9 tháng 7 2019
\(\sqrt{25x^2-10x+1}=4x+9\)
\(\Leftrightarrow\sqrt{\left(5x-1\right)^2}=4x+9\)
\(\Leftrightarrow\left|5x-1\right|=4x+9\)
\(\Leftrightarrow\orbr{\begin{cases}5x-1=4x+9\\5x-1=-4x-9\end{cases}\Leftrightarrow\orbr{\begin{cases}x=10\\x=-\frac{8}{9}\end{cases}}}\)
Vậy ...
HN
9 tháng 7 2019
\(\sqrt{x^2+2x+1}=\sqrt{x+1}\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}=\sqrt{x+1}\)
\(\Leftrightarrow\sqrt{\left(x+1\right)^2}-\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{x+1}.\left(\sqrt{x+1}-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x+1}=0\\\sqrt{x+1}-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=0\end{cases}}}\)
Vậy ...
21 tháng 8 2023
a: \(\Leftrightarrow2\cdot5\sqrt{x-3}-\dfrac{1}{2}\cdot2\sqrt{x-3}+\dfrac{1}{7}\cdot7\sqrt{x-3}=20\)
=>\(10\cdot\sqrt{x-3}=20\)
=>\(\sqrt{x-3}=2\)
=>x-3=4
=>x=7
b: =>|x-3|=2
=>x-3=2 hoặc x-3=-2
=>x=5 hoặcx=1
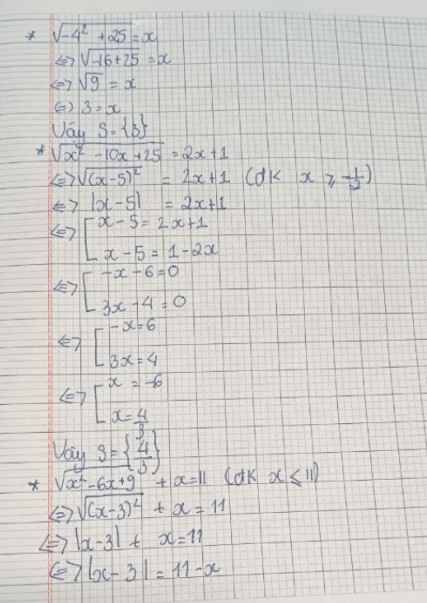
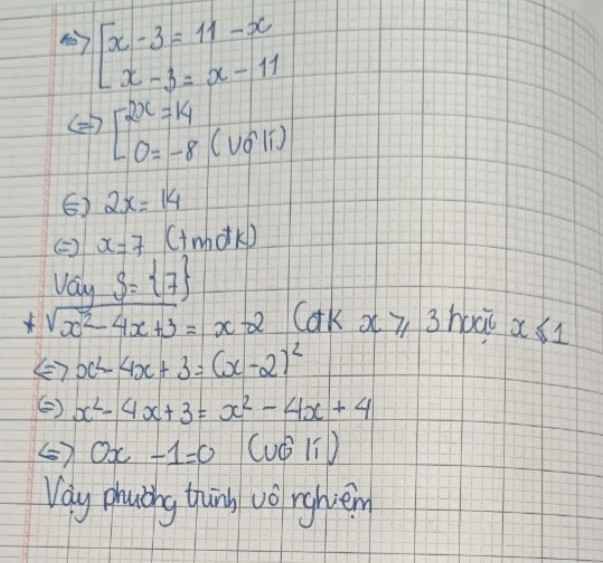
Ta có: \(\sqrt{x^2-6x+9}+\sqrt{x^2+10x+25}=8\)
\(\Rightarrow\sqrt{\left(x-3\right)^2}+\sqrt{\left(x+5\right)^2}=8\)
\(\Rightarrow x-3+x+5=8\)
\(\Rightarrow2x=6\Rightarrow x=3\)
\(\sqrt{x^2-6x+9}+\sqrt{x^2+10x+25}=8\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}+\sqrt{\left(x+5\right)^2}=8\Leftrightarrow\left|x-3\right|+\left|x+5\right|=8\) (1)
Nếu \(x< -5\) thì (1) trở thành:
\(3-x+\left(-x-5\right)=8\Leftrightarrow-2x-2=8\Leftrightarrow x=-5\) (loại)
-Nếu \(-5\le x< 3\) thì (1) trở thành:
\(3-x+x+5=8\Leftrightarrow8=8\)
-Nếu \(x>3\) thì (1) trở thành:
\(x-3+x+5=8\Leftrightarrow2x+2=8\Leftrightarrow x=3\) (thỏa mãn)
Vậy \(-5\le x\le3\)