DN
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H9
HT.Phong (9A5)
CTVHS
24 tháng 9 2023
a) \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}+2=0\) (ĐK: \(x\ge1\))
\(\Leftrightarrow\sqrt{x-1}+\sqrt{4\left(x-1\right)}-\sqrt{25\left(x-1\right)}+2=0\)
\(\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}+2=0\)
\(\Leftrightarrow-2\sqrt{x-1}=-2\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{2}{2}\)
\(\Leftrightarrow\sqrt{x-1}=1\)
\(\Leftrightarrow x-1=1\)
\(\Leftrightarrow x=2\left(tm\right)\)
b) \(\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}=16\) (ĐK: \(x\ge-1\))
\(\Leftrightarrow\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}+\sqrt{4\left(x+1\right)}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}=16\)
\(\Leftrightarrow\sqrt{x+1}=4\)
\(\Leftrightarrow x+1=16\)
\(\Leftrightarrow x=15\left(tm\right)\)
TN
1
15 tháng 10 2021
\(a,PT\Leftrightarrow\left|3x-1\right|=\left|x-3\right|\Leftrightarrow\left[{}\begin{matrix}3x-1=x-3\\3x-1=3-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\\ b,PT\Leftrightarrow\left|x-4\right|=4-x\Leftrightarrow\left[{}\begin{matrix}x-4=4-x\left(x\ge4\right)\\x-4=x-4\left(x< 4\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=0\left(tm\right)\end{matrix}\right.\)
VN
2
TN
10 tháng 12 2018
Ta có: \(\sqrt{x^2-6x+9}+\sqrt{x^2+10x+25}=8\)
\(\Rightarrow\sqrt{\left(x-3\right)^2}+\sqrt{\left(x+5\right)^2}=8\)
\(\Rightarrow x-3+x+5=8\)
\(\Rightarrow2x=6\Rightarrow x=3\)
10 tháng 12 2018
\(\sqrt{x^2-6x+9}+\sqrt{x^2+10x+25}=8\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}+\sqrt{\left(x+5\right)^2}=8\Leftrightarrow\left|x-3\right|+\left|x+5\right|=8\) (1)
Nếu \(x< -5\) thì (1) trở thành:
\(3-x+\left(-x-5\right)=8\Leftrightarrow-2x-2=8\Leftrightarrow x=-5\) (loại)
-Nếu \(-5\le x< 3\) thì (1) trở thành:
\(3-x+x+5=8\Leftrightarrow8=8\)
-Nếu \(x>3\) thì (1) trở thành:
\(x-3+x+5=8\Leftrightarrow2x+2=8\Leftrightarrow x=3\) (thỏa mãn)
Vậy \(-5\le x\le3\)
3 tháng 8 2017
a) giải pt ra ta được : x=-1
b) giải pt ra ta được : x=2
c)giải pt ra ta được : x vô ngiệm
d)giải pt ra ta được : x=vô ngiệm
~~~~~~~~~~~ai đi ngang qua nhớ để lại k ~~~~~~~~~~~~~
~~~~~~~~~~~~ Chúc bạn sớm kiếm được nhiều điểm hỏi đáp ~~~~~~~~~~~~~~~~~~~
TN
4 tháng 10 2017
Vừa làm bên Học 24 xong nhưng do gửi link thì bị lỗi nên t up lại, tiện thể ăn điểm luôn (tất nhiên giúp you vẫn là lí do chính, điểm là tiện thôi :))
\(pt\left(2\right)\Leftrightarrow\sqrt{2\left(x-y\right)^2+10x-6y+12}-\sqrt{y}-\sqrt{x+2}=0\)
\(\Leftrightarrow\sqrt{2\left(x-y\right)^2+10x-6y+12}-2\sqrt{y}-\left(\sqrt{x+2}-\sqrt{y}\right)=0\)
\(\Leftrightarrow\frac{2\left(x-y\right)^2+10x-6y+12-4y}{\sqrt{2\left(x-y\right)^2+10x-6y+12}+2\sqrt{y}}-\frac{x+2-y}{\sqrt{x+2}+\sqrt{y}}=0\)
\(\Leftrightarrow\frac{2\left(x-y+3\right)\left(x-y+2\right)}{\sqrt{2\left(x-y\right)^2+10x-6y+12}+2\sqrt{y}}-\frac{x-y+2}{\sqrt{x+2}+\sqrt{y}}=0\)
\(\Leftrightarrow\left(x-y+2\right)\left(\frac{2\left(x-y+3\right)}{\sqrt{2\left(x-y\right)^2+10x-6y+12}+2\sqrt{y}}-\frac{1}{\sqrt{x+2}+\sqrt{y}}\right)=0\)
\(\Rightarrow x=y-2\). Thay vào \(pt\left(1\right)\) ta có:
\(pt\left(1\right)\Leftrightarrow\sqrt{y^2-8\left(y-2\right)+9}-\sqrt[3]{\left(y-2\right)y+12-6\left(y-2\right)}\le1\)
\(\Leftrightarrow\sqrt{y^2-8y+25}-\sqrt[3]{y^2-8y+24}\le1\)
\(\Leftrightarrow\left(\sqrt{y^2-8y+25}-3\right)-\left(\sqrt[3]{y^2-8y+24}-2\right)\le0\)
\(\Leftrightarrow\frac{y^2-8y+25-9}{\sqrt{y^2-8y+25}+3}-\frac{y^2-8y+24-8}{\sqrt[3]{\left(y^2-8y+24\right)^2}+4+2\sqrt[3]{y^2-8y+24}}\le0\)
\(\Leftrightarrow\frac{\left(y-4\right)^2}{\sqrt{y^2-8y+25}+3}-\frac{\left(y-4\right)^2}{\sqrt[3]{\left(y^2-8y+24\right)^2}+4+2\sqrt[3]{y^2-8y+24}}\le0\)
\(\Leftrightarrow\left(y-4\right)^2\left(\frac{1}{\sqrt{y^2-8y+25}+3}-\frac{1}{\sqrt[3]{\left(y^2-8y+24\right)^2}+4+2\sqrt[3]{y^2-8y+24}}\right)\le0\)
\(\Rightarrow y=4\Rightarrow x=y-2=4-2=2\)
Vậy \(x=2;y=4\)
14 tháng 2 2016
câu a) chuyển sang vế trái nhóm hằng đẳng thức
b) bình lên cho nhanh
c) chứng minh cái VT>=6 VÀ VP<=6
PA
28 tháng 9 2017
a)
\(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+21}=5-2x-x^2\)
\(\Leftrightarrow\sqrt{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+16}=6-\left(x+1\right)^2\)
\(VT\ge6;VP\le6\Rightarrow VT=VP=6\)
Vậy pt có một nghiệm duy nhất là \(x=-1\)
b)
\(\sqrt{4x^2+20x+25}+\sqrt{x^2-8x+16}=\sqrt{x^2+18x+81}\)
\(\Leftrightarrow\sqrt{\left(2x+5\right)^2}+\sqrt{\left(x-4\right)^2}=\sqrt{\left(x+9\right)^2}\)
\(\Leftrightarrow\left|2x+5\right|+\left|x-4\right|=\left|x+9\right|\)
Lập bảng xét dấu ra nhé ~^o^~
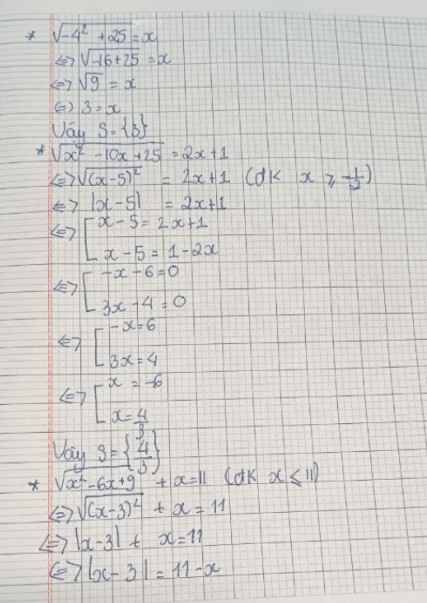
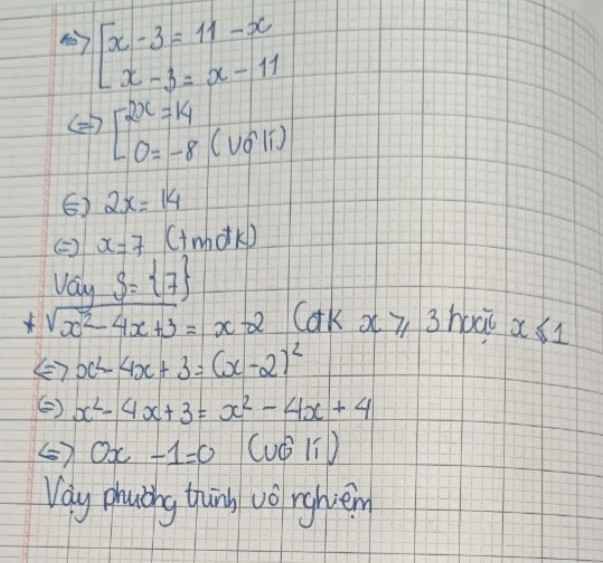
=>\(\sqrt{\left(x+3\right)^2}\)+ \(\sqrt{\left(x+4\right)^2}\)+\(\sqrt{\left(x+5\right)^2}\)=9x
=> x + 3 + x + 4 + x + 5 = 9x
=> - 6x = - 12
=> x=2
Ủa sao phá đc trị tuyệt đối hay v bạn? (căn a^2 = trị tuyệt đối của a )