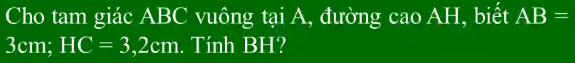Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng hệ thức lượng trong tam giác vuông ABC :
\(AB^2=HB\cdot BC\)
\(\Leftrightarrow AB^2=HB\cdot\left(HB+HC\right)\)
\(\Leftrightarrow3^2=HB^2+3.2HB\)
\(\Leftrightarrow HB^2+3.2HB-9=0\)
\(\Leftrightarrow\left[{}\begin{matrix}HB=1.8\left(N\right)\\HB=-5\left(L\right)\end{matrix}\right.\)
Ta có: \(BH+HC=BC\Rightarrow BC=BH+3,2\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\)
\(\Leftrightarrow3^2=BH.\left(BH+3,2\right)\)
\(\Leftrightarrow BH^2+3,2BH-9=0\) (bấm máy phương trình bậc 2: \(x^2+3,2x-9=0\))
\(\Rightarrow\left[{}\begin{matrix}BH=-5< 0\left(loại\right)\\BH=1,8\end{matrix}\right.\)
Vậy \(BH=1,8\left(cm\right)\)

\(\sqrt{\left(2-\sqrt{3}\right)\left(\sqrt{6+\sqrt{2}}\right)}=2\)
=2.

"Hình như" ở 2 mẫu phải cùng là số 2 hoặc -2 vì theo đó, phương trình sẽ có dạng giải được. Mình sửa lại đề theo hướng đó!
\(x=0\) không phải là nghiệm của pt
Xét \(x\ne0\), chia cả tử và mẫu 2 phân số đầu cho x, ta được:
\(pt\Leftrightarrow\frac{2}{3x+\frac{2}{x}-1}-\frac{7}{3x+\frac{2}{x}+5}=1\)
Đặt \(t=3x+\frac{2}{x}\)
\(pt\rightarrow\frac{2}{t-1}-\frac{7}{t+5}=1\Leftrightarrow t\in\left\{-11;2\right\}\)
Thay lại giải ra x.

Ta có : \(4,5.\sqrt{\dfrac{8}{3}}=\dfrac{9}{2}.\sqrt{\dfrac{8}{3}}=\sqrt{\left(\dfrac{9}{2}\right)^2}.\sqrt{\dfrac{8}{3}}=\sqrt{\dfrac{81}{4}.\dfrac{8}{3}}=\sqrt{54}\)

\(a,=\dfrac{\sqrt{2}\left(1+\sqrt{2}\right)}{1+\sqrt{2}}=\sqrt{2}\\ b,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{5}\\ c,=\dfrac{\sqrt{3}\left(1-\sqrt{2}\right)}{2\left(\sqrt{2}-1\right)}=-\dfrac{\sqrt{3}}{2}\\ d,=\dfrac{\sqrt{5}\left(1-\sqrt{2}\right)}{\sqrt{3}\left(1-\sqrt{2}\right)}=\dfrac{\sqrt{5}}{\sqrt{3}}=\dfrac{\sqrt{15}}{3}\\ e,=\dfrac{\sqrt{7}\left(\sqrt{7}+1\right)}{\sqrt{7}+1}=\sqrt{7}\\ f,=\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}=\sqrt{5}\\ g,=\dfrac{\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}=\sqrt{2}\\ h,=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{5}\)