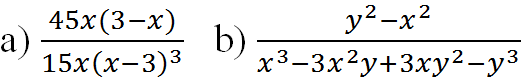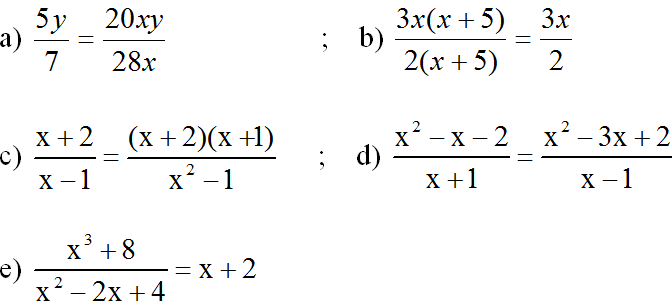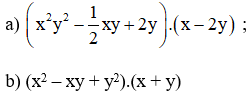K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PQ
1
LA
6 tháng 12 2016
Bài 16. Giải thích vì sao diện tích của tam giác được tô đậm trong các hình 128,129, 130 bằng nửa diện tích hình chữ nhật tương ứng:
Hướng dẫn giải:
Ở mỗi hình 128, 129, 130; hình tam giác và hình chữ nhật đều có cùng đáy a và cùng chiều cao h nên diện tích của tam giác bằng nửa diện tích hình chữ nhật tương ứng.
tk nha bạn
thank you bạn
HH
26 tháng 2 2020
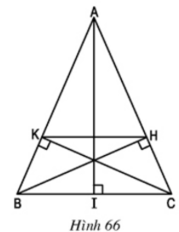
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
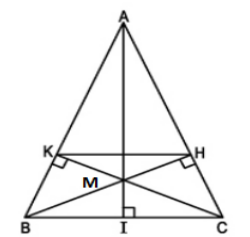
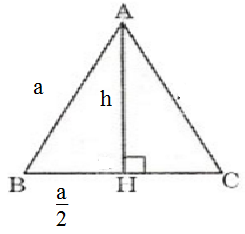
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)
8 tháng 10 2019
Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
8 tháng 10 2019
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
29 tháng 9 2015
a) Tứ giác ABCD là hình bình hành => AB//CD
mà AK=1/2AB(gt)
IC=1/2DC(gt)
nên tứ giác ABCD là hình bình hành (tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau).
Do đó AI // CK(hai cạnh đối của hình bình hành)
b) ∆DCN có DI = IC(gt)
IM // CN(IA//KC,M thuộc AI,N thuộc KC)
vậy M là trung điểm của DN=>DM = MN(1)
Xét ∆ABM ta có AK=KB(gt)
NK//MK(AI//KC,M thuộc AI,N thuộc KC) => N là trung điểm của MB=> NM=NB (2)
từ (1)+(2)=> DM = MN = NB
H
4
21 tháng 9 2018
-
Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
- Chứng Tỏ Rằng J Hả Bạn ??????
31 tháng 12 2018
Hỏi công thức à !
1 ) muốn nhân 2 số tự nhiên có 1 chữ số ta lấy hai số nhân vs nhau
2 ) muốn nhân 2 số tự nhiên có 2 chữ số ta lấy hai số nhân vs nhau
3 ) muốn nhân 2 số tự nhiên có 100 chữ số ta lấy máy tính bấm ra kết quả ( 100 số tính tay xong thì liệt luôn )