
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi chiều rộng của hình chữ nhật là x>0 (m)
Chiều dài hình chữ nhật: \(x+10\) (m)
Nửa chu vi hình chữ nhật: \(\dfrac{100}{2}=50\left(m\right)\)
Ta có pt:
\(x+\left(x+10\right)=50\)
\(\Leftrightarrow2x=40\Rightarrow x=20\) (m)
Vậy hình chữ nhật rộng 20m, dài 30m

8) \(\dfrac{x+7}{3}+\dfrac{x+5}{4}=\dfrac{x+3}{5}+\dfrac{x+1}{6}\)
\(\Rightarrow\dfrac{x+7}{3}+\dfrac{x+5}{4}-\dfrac{x+3}{5}-\dfrac{x+1}{6}=0\)
\(\Rightarrow\dfrac{x+7}{3}+2+\dfrac{x+5}{4}+2-\dfrac{x+3}{5}-2-\dfrac{x+1}{6}-2=0+2+2-2-2\)
\(\Rightarrow\left(\dfrac{x+7}{3}+2\right)+\left(\dfrac{x+5}{4}+2\right)-\left(\dfrac{x+3}{5}+2\right)-\left(\dfrac{x+1}{6}+2\right)=0\)
\(\Rightarrow\left(\dfrac{x+7}{3}+\dfrac{6}{3}\right)+\left(\dfrac{x+5}{4}+\dfrac{8}{4}\right)-\left(\dfrac{x+3}{5}+\dfrac{10}{5}\right)-\left(\dfrac{x+1}{6}+\dfrac{12}{2}\right)=0\)
\(\Rightarrow\left(x+13\right)\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}-\dfrac{1}{6}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+13=0\\\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\end{matrix}\right.\)
\(x+13=0\)
\(\Rightarrow x=-13\)
\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\)
\(\dfrac{13}{60}=0\) (vô lí)
Vậy \(x=-13\)
9) Bạn chuyển vế rồi cộng 3 vào từng mỗi số

Lời giải:
a) Theo tính chất tia phân giác ta có:
$\frac{EM}{EN}=\frac{DM}{DN}=\frac{2DM}{NP}(1)$
$\frac{FM}{FP}=\frac{DM}{DP}=\frac{2DM}{NP}(2)$
Từ $(1);(2)\Rightarrow \frac{EM}{EN}=\frac{FM}{FP}$
Theo định lý Talet đảo suy ra $EF\parallel NP$
b)
$G$ là điểm nào bạn?
GIẢI PHƯƠNG TRÌNH :
\(\left(3x+5\right)^2-\left(2x+1\right)^2=0\)
giải hộ e vs ạ !!!
e cảm ơn nhìu :3

(3x + 5)2 - (2x + 1)2 = 0
<=> (3x + 5 + 2x + 1)(3x + 5 - 2x - 1) = 0
<=> (5x + 6)(x + 4) = 0
<=> \(\orbr{\begin{cases}x=-\frac{6}{5}\\x=-4\end{cases}}\)
Vậy \(x\in\left\{-\frac{6}{5};-4\right\}\)là nghiệm phương trình
\(\left(3x+5\right)^2-\left(2x+1\right)^2=0\)
\(\Leftrightarrow\left(3x+5+2x+1\right)\left(3x+5-2x-1\right)=0\)
\(\Leftrightarrow\left(5x+6\right)\left(x+4\right)=0\Leftrightarrow x=-4;x=-\frac{6}{5}\)
Vậy tập nghiệm của phương trình là S = { -4 ; -6/5 }

Ta có: \(\dfrac{150}{x+10}-\dfrac{150}{x}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{300x}{2x\left(x+10\right)}-\dfrac{300\left(x+10\right)}{2x\left(x+10\right)}=\dfrac{x\left(x+10\right)}{2x\left(x+10\right)}\)
\(\Leftrightarrow x^2+10x=300x-300x-3000\)
\(\Leftrightarrow x^2+10x+3000=0\)
\(\Leftrightarrow x^2+10x+25+2975=0\)
\(\Leftrightarrow\left(x+5\right)^2+2975=0\)(Vô lý)

a, Đặt \(A=2+x-x^2=-\left(x^2-x-2\right)=-\left(x^2-x+\frac{1}{4}-\frac{9}{4}\right)=-\left(x-\frac{1}{2}\right)^2+\frac{9}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\Rightarrow-\left(x-\frac{1}{2}\right)^2\le0\Rightarrow A=-\left(x-\frac{1}{2}\right)^2+\frac{9}{4}\le\frac{9}{4}\)
Dấu "=" xảy ra khi x = 1/2
Vậy Amax=9/4 khi x=1/2
b, Đặt \(B=4x^2-20x+26=\left(2x\right)^2-2.2x.5+25+1=\left(2x-5\right)^2+1\)
Vì \(\left(2x-5\right)^2\ge0\Rightarrow B=\left(2x-5\right)^2+1\ge1\)
Dấu "=" xảy ra khi x = 5/2
Vậy Bmin=1 khi x=5/2

Bài Giải
Tam giác ABC có cạnh huyền PC là 1 cạnh của tam giác PQC
Xét tam giác QMC và tam giác BMN có :
BM=MC
Góc BMN=góc QMC
QM=MN
=>Tam giác BMN=tam giác QMC
=>BN=QC(hai góc tương ứng)
MÌNH CHỈ GIẢI ĐC ĐẾN ĐÂY THÔI




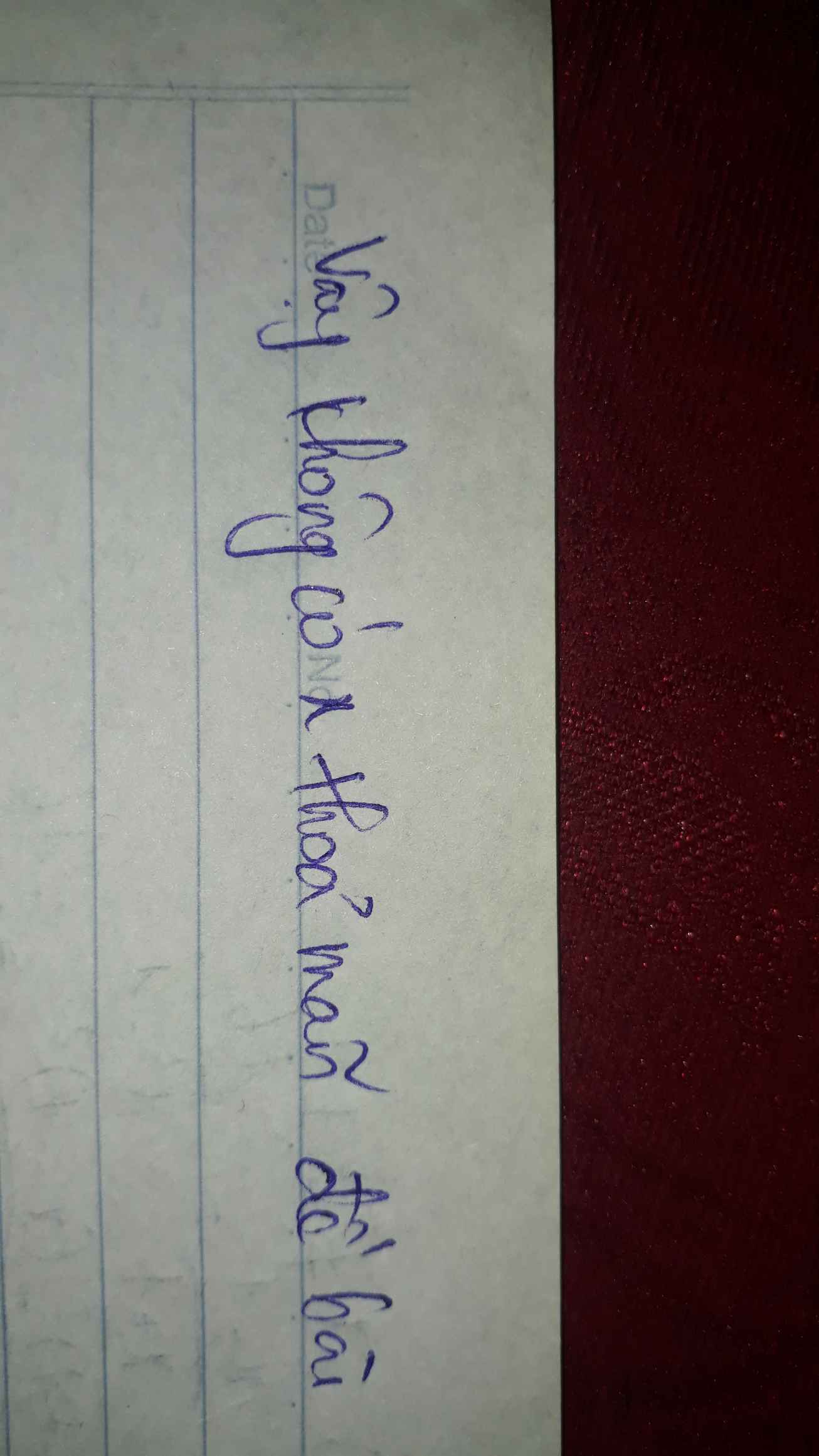
Bài 5:
Áp dụng BĐT Cô-si cho các số không âm:
$a^4+b^4\geq 2a^2b^2$
$c^4+d^4\geq 2c^2d^2$
$2(a^2b^2+c^2d^2)\geq 4\sqrt{a^2b^2c^2d^2}=4|abcd|\geq 4abcd$
$\Rightarrow a^4+b^4+c^4+d^4\geq 4abcd$
Ta có đpcm
Dấu "=" xảy ra khi $|a|=|b|=|c|=|d|$ và $ab=cd$
Bài 1:
Đổi $30$ phút thành $0,5$ giờ
Thời gian đi từ $A$ đến $B$ là:
$t_1=\frac{AB}{40}$ (h)
Thời gian đi từ $B$ về $A$ là:
$t_2=\frac{BA}{45}$ (h)
Theo bài ra ta có:
$t_1-t_2=\frac{AB}{40}-\frac{AB}{45}$
$0,5=\frac{AB}{360}$
$\Rightarrow AB=180$ (km)