K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
2
HL
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 11 2021
1.1
Pt có 2 nghiệm trái dấu và tổng 2 nghiệm bằng -3 khi:
\(\left\{{}\begin{matrix}ac< 0\\x_1+x_2=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(m+2\right)< 0\\\dfrac{2m+1}{m+2}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m=-\dfrac{7}{5}\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
b.
Pt có nghiệm kép khi:
\(\left\{{}\begin{matrix}m+2\ne0\\\Delta=\left(2m+1\right)^2-8\left(m+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m^2-4m-15=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)
TD
1
30 tháng 6 2023
8:
\(=\dfrac{cos10-\sqrt{3}\cdot sin10}{sin10\cdot cos10}=\dfrac{2\left(\dfrac{1}{2}\cdot cos10-\dfrac{\sqrt{3}}{2}\cdot sin10\right)}{sin20}=\dfrac{sin\left(30-10\right)}{sin20}=1\)
10:
\(=\left(2-\sqrt{3}\right)^2+\left(2+\sqrt{3}\right)^2\)
=7-4căn 3+7+4căn 3=14
12:
\(=cos^270^0+\dfrac{1}{2}\left[cos60-cos140\right]\)
\(=cos^270^0+\dfrac{1}{2}\cdot\dfrac{1}{2}-\dfrac{1}{2}\cdot2cos^270^0+\dfrac{1}{.2}\)
=1/4+1/2=3/4
LT
2
AN
30 tháng 10 2017
Xét đồ thị thấy x = 2 -> y = 0
và x = -2 -> y = 0
Nên f(x) = f (-x ) -> Chọn A
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
Lời giải:
a. TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(x)=|x|=|-x|=f(-x)$
$\Rightarrow $ hàm chẵn
b. TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=9; -f(1)=-9; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$ nên hàm không chẵn không lẻ.
c.
TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(-x)=(-x)^3+(-x)=-(x^3+x)=-f(x)$ nên hàm lẻ
d.
TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=3; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$
Do đó hàm không chẵn không lẻ.
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
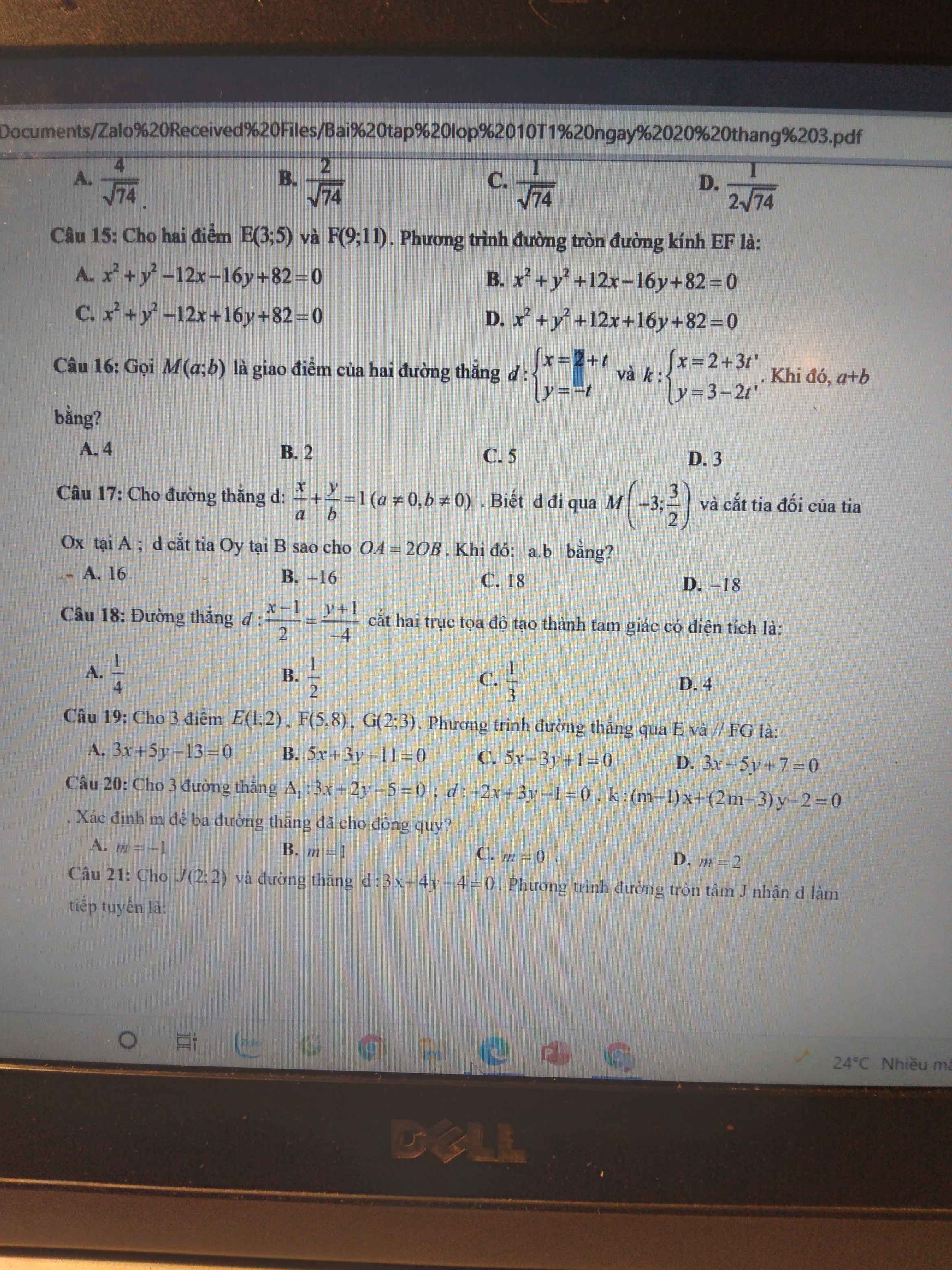
16.
Hệ tọa độ giao điểm: \(\left\{{}\begin{matrix}2+t=2+3t'\\-t=3-2t'\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}t=-9\\t'=-3\end{matrix}\right.\)
Thay \(t=-9\) vào pt d ta được: \(\left\{{}\begin{matrix}a=-7\\b=9\end{matrix}\right.\)
\(\Rightarrow a+b=2\)
17.
Do d qua M nên: \(\dfrac{-3}{a}+\dfrac{3}{2b}=1\) (1)
d cắt tia đối Ox tại A \(\Rightarrow a< 0\) và \(OA=-a\)
d cắt Oy tại b \(\Rightarrow b>0\) và \(OB=b\)
\(OA=2OB\Rightarrow-a=2b\)
Thế vào (1): \(\dfrac{-3}{a}+\dfrac{3}{-a}=1\Rightarrow a=-6\Rightarrow b=\dfrac{-a}{2}=3\)
\(\Rightarrow ab=-18\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
18.
Gọi A là giao điểm của d với Ox
\(\Rightarrow y_A=0\Rightarrow\dfrac{x_A-1}{2}=\dfrac{0+1}{-4}\Rightarrow x_A=\dfrac{1}{2}\)
\(\Rightarrow OA=\left|x_A\right|=\dfrac{1}{2}\)
Gọi B là giao điểm của d với Oy
\(\Rightarrow x_B=0\Rightarrow\dfrac{0-1}{2}=\dfrac{y_B+1}{-4}\Rightarrow y_B=1\)
\(\Rightarrow OB=\left|y_B\right|=1\)
\(S=\dfrac{1}{2}OA.OB=\dfrac{1}{4}\)
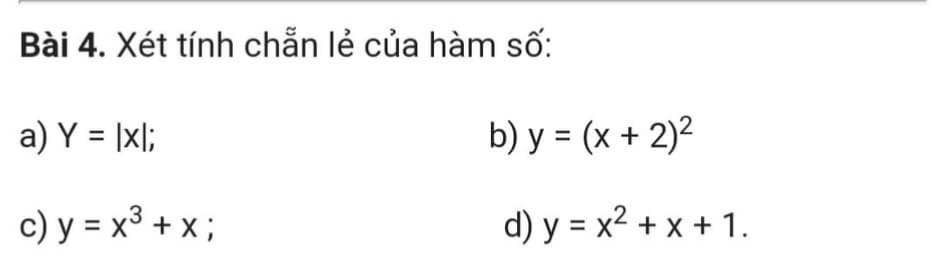
Đồ thị hướng lên nên a > 0 => Loại A,B
Dựa vào đồ thị, A( 1; 0) thuộc đồ thị => Chọn C