K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
2
H9
HT.Phong (9A5)
CTVHS
6 tháng 7 2023
Bài 2:
a) \(\dfrac{2}{15}-\dfrac{7}{10}=\dfrac{4}{30}-\dfrac{21}{30}=-\dfrac{17}{30}\)
b) \(\dfrac{-3}{14}+\dfrac{2}{21}=\dfrac{-9}{42}+\dfrac{4}{42}=\dfrac{-5}{42}\)
c) \(\dfrac{-6}{9}+\dfrac{-12}{16}=\dfrac{-96}{144}+\dfrac{-108}{144}=\dfrac{-204}{144}=-\dfrac{17}{12}\)
H9
HT.Phong (9A5)
CTVHS
6 tháng 7 2023
Bài 3:
a) \(\dfrac{3}{8}+\dfrac{-5}{6}=\dfrac{3}{8}-\dfrac{5}{6}=\dfrac{18}{48}-\dfrac{40}{48}=-\dfrac{22}{48}=-\dfrac{11}{24}\)
b) \(\dfrac{-8}{18}-\dfrac{15}{27}=\dfrac{-24}{54}-\dfrac{30}{54}=\dfrac{-54}{54}=-1\)
c) \(\dfrac{2}{21}-\dfrac{-1}{28}=\dfrac{8}{84}-\dfrac{-3}{84}=\dfrac{11}{84}\)
22 tháng 10 2021
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{d}{5}=\dfrac{a+b+c+d}{2+3+4+5}=\dfrac{140}{14}=10\)
Do đó: a=20; b=30; c=40; d=50
8 tháng 2 2023
Bài 6:
Gọi độ dài hai cạnh lần lượt là a,b
Theo đề, ta có: a/3=b/5 và a+b=24
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{24}{8}=3\)
=>a=9; b=15
HN
0
A
9 tháng 8 2021
\(\frac{1}{3}x-\frac{3}{5}=\frac{5}{6}x+2\)
\(\Leftrightarrow\frac{x}{3}-\frac{3}{5}=\frac{5x}{6}+2\)
\(\Leftrightarrow2x-\frac{18}{5}=5x+12\)
\(\Leftrightarrow2x-5x=\frac{18}{5}+12\)
\(\Leftrightarrow-3x=\frac{78}{5}\)
\(\Leftrightarrow3x=-\frac{78}{5}\)
\(\Leftrightarrow x=-\frac{26}{5}\)
Ps: đoạn nào không hiểu hỏi anh nhé. Nhớ k để tạo động lực cho anh nhé :33
# Aeri #
15 tháng 7 2021
a) Ta có: O nằm trên đường trung trực của MN(gt)
nên OM=ON(1)
Ta có: O nằm trên đường trung trực của MP(gt)
nên OM=OP(2)
Từ (1) và (2) suy ra ON=OP
b) Xét ΔONM có OM=ON(cmt)
nên ΔOMN cân tại O(Định nghĩa tam giác cân)
mà Ox là đường trung trực ứng với cạnh đáy MN
nên Ox là tia phân giác của \(\widehat{MON}\)
Xét ΔOMP có OM=OP(cmt)
nên ΔOMP cân tại O(Định nghĩa tam giác cân)
mà Oy là đường trung trực ứng với cạnh đáy MP
nên Oy là tia phân giác của \(\widehat{POM}\)
Ta có: \(\widehat{NOM}+\widehat{POM}=\widehat{PON}\)
\(\Leftrightarrow\widehat{PON}=2\cdot\left(\widehat{xOM}+\widehat{yOM}\right)=2\cdot90^0=180^0\)
hay P,O,N thẳng hàng(đpcm)
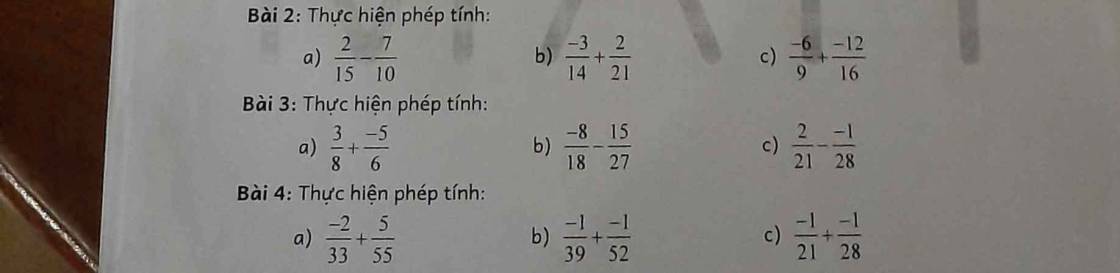
Bài 1:
1: \(20x^5:5x=\left(20:5\right)\cdot\left(x^5:x\right)=4x^4\)
2: \(12x^4:6x^3=\left(12:6\right)\cdot\left(x^4:x^3\right)=2x\)
3: \(35x^7:5x^3=\left(35:5\right)\cdot\left(x^7:x^3\right)=7x^4\)
4: \(\dfrac{21x^{12}}{3x^2}=\dfrac{21}{3}\cdot\dfrac{x^{12}}{x^2}=7x^{10}\)
5: \(\dfrac{14x^4}{3x^2}=\dfrac{14}{3}\cdot\dfrac{x^4}{x^2}=\dfrac{14}{3}x^2\)
6: \(\dfrac{15x^5}{7x^3}=\dfrac{15}{7}\cdot\dfrac{x^5}{x^3}=\dfrac{15}{7}x^2\)
7: \(\dfrac{22x^7}{4x}=\dfrac{22}{4}\cdot\dfrac{x^7}{x}=5,5x^6\)
8: \(18x^6:2x^6=\dfrac{18}{2}\cdot\dfrac{x^6}{x^6}=9\)
9: \(-30x^6:\dfrac{3}{4}x^5=\left(-30:\dfrac{3}{4}\right)\cdot\left(x^6:x^5\right)=-40x\)
10: \(9x^9:\left(\dfrac{3}{10}x^3\right)=\left(9:\dfrac{3}{10}\right)\cdot\left(x^9:x^3\right)=30x^6\)
11: \(-6x^8:\left(\dfrac{3}{7}x^4\right)=\left(-6:\dfrac{3}{7}\right)\cdot\left(x^8:x^4\right)=-14x^4\)
12: \(4x^{20}:\left(-\dfrac{2}{5}x^{10}\right)=\left(4:\dfrac{-2}{5}\right)\cdot\left(x^{20}:x^{10}\right)=-10x^{10}\)