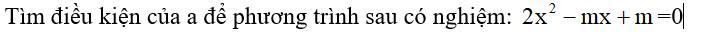K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 5 2023
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔACE và ΔAFC có
góc ACE=góc AFC
góc CAE chung
=>ΔACE đồng dạng với ΔAFC
=>AC^2=AE*AF
Y
23 tháng 2 2023
\(b,\) Với giá trị đã tim được ở câu a, ta tiếp tục làm câu b
\(A-\dfrac{2}{\sqrt{3}}=\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{3}}\)\(\left(1\right)\)
Thay \(x=7+4\sqrt{3}\) vào \(\left(1\right)\)
\(\Rightarrow\dfrac{\sqrt{7+4\sqrt{3}}}{\sqrt{7+4\sqrt{3}}-2}-\dfrac{2}{\sqrt{3}}\)
\(=1\)
3 tháng 3 2023
Ta có:
\(\Delta=b^2-4ac=\left(-m\right)^2-4.2.m\) \(=m^2-8m\)
Để phương trình có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow m^2-8m\ge0\Leftrightarrow\left[{}\begin{matrix}m\le0\\m\ge8\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
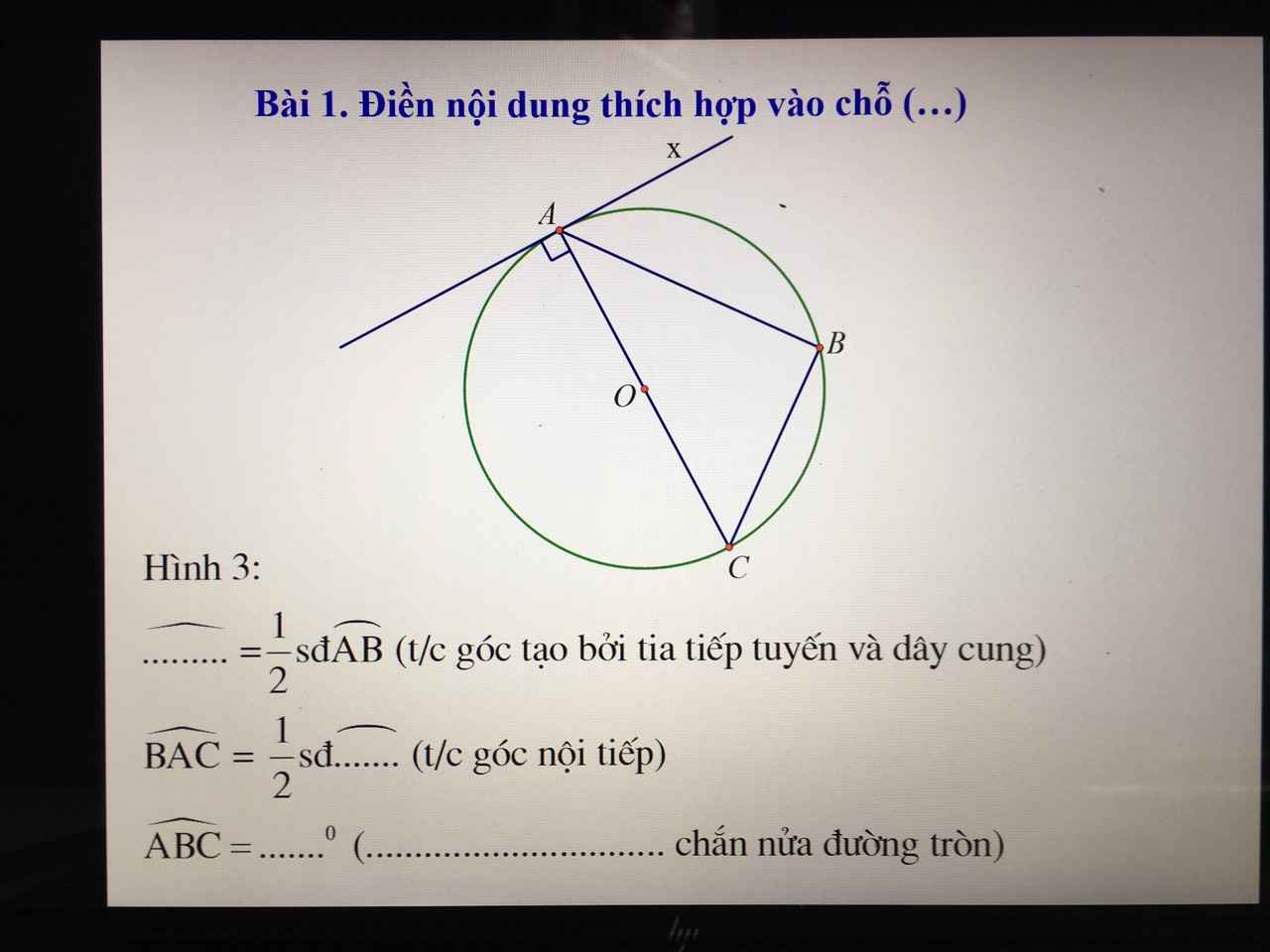
\(\widehat{BAx}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
\(\widehat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\)
\(\widehat{ABC}=90^0\) (góc nội tiếp chắn nửa đường tròn)
QN
0
26 tháng 8 2021
\(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\left(đk:x\ge0,x\ne9\right)\)
Để \(M=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}< 0\) thì
\(\sqrt{x}-3< 0\) ( do \(\sqrt{x}+3\ge3>0\))
\(\Leftrightarrow\sqrt{x}< 3\Leftrightarrow0\le x< 9\)
Mà \(x\in Z\)
\(\Rightarrow x\in\left\{0;1;2;3;4;5;6;7;8\right\}\)
DM
1
17 tháng 2 2022
\(\left\{{}\begin{matrix}x+y=5\\\dfrac{3}{5}+\dfrac{2}{x-y}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=5\\\dfrac{2}{x-y}=\dfrac{12}{5}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x+y=5\\6\left(x-y\right)=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=5\\x-y=\dfrac{5}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=\dfrac{35}{6}\\y=x-\dfrac{5}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{35}{12}\\y=\dfrac{25}{12}\end{matrix}\right.\)
H
1