
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ

a) Vì \(\left|2x+4\right|\ge0;\left|y\right|\ge0\)
mà \(\left|2x+4\right|+\left|y\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|2x+4\right|=0\\\left|y\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(-2;0\right)\)


3:
a: Xét ΔOAB có
OH vừa là đường cao, là phân giác
Do đó: ΔOAB cân tại O
b: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
Xét ΔCAB có
CH vừa là đường cao, vừa là trung tuyến
Do đó: ΔCAB cân tại C
c: OE+EA=OA
OD+DB=OB
mà OE=OD và OA=OB
nên EA=DB
Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
Do đó: ΔOAC=ΔOBC
=>góc OAC=góc OBC
=>góc DBC=góc EAC
Xét ΔDBC và ΔEAC có
góc CDB=góc CEA
DB=EA
góc CBD=góc CAE
Do đó: ΔDBC=ΔEAC
=>góc ECA=góc DCB
=>góc ECA+góc BCA=180 độ
=>B,C,E thẳng hàng

a) Xét ΔADB và ΔADC có
AB=AC(gt)
AD chung
DB=DC(D là trung điểm của BC)
Do đó: ΔADB=ΔADC(c-c-c)
b) Ta có: AB=AC(gt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DB=DC(D là trung điểm của BC)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AD là đường trung trực của BC
hay AD⊥BC(đpcm)
c) Ta có: CE⊥BC(gt)
AD⊥BC(cmt)
Do đó: EC//AD(Định lí 1 từ vuông góc tới song song)





 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn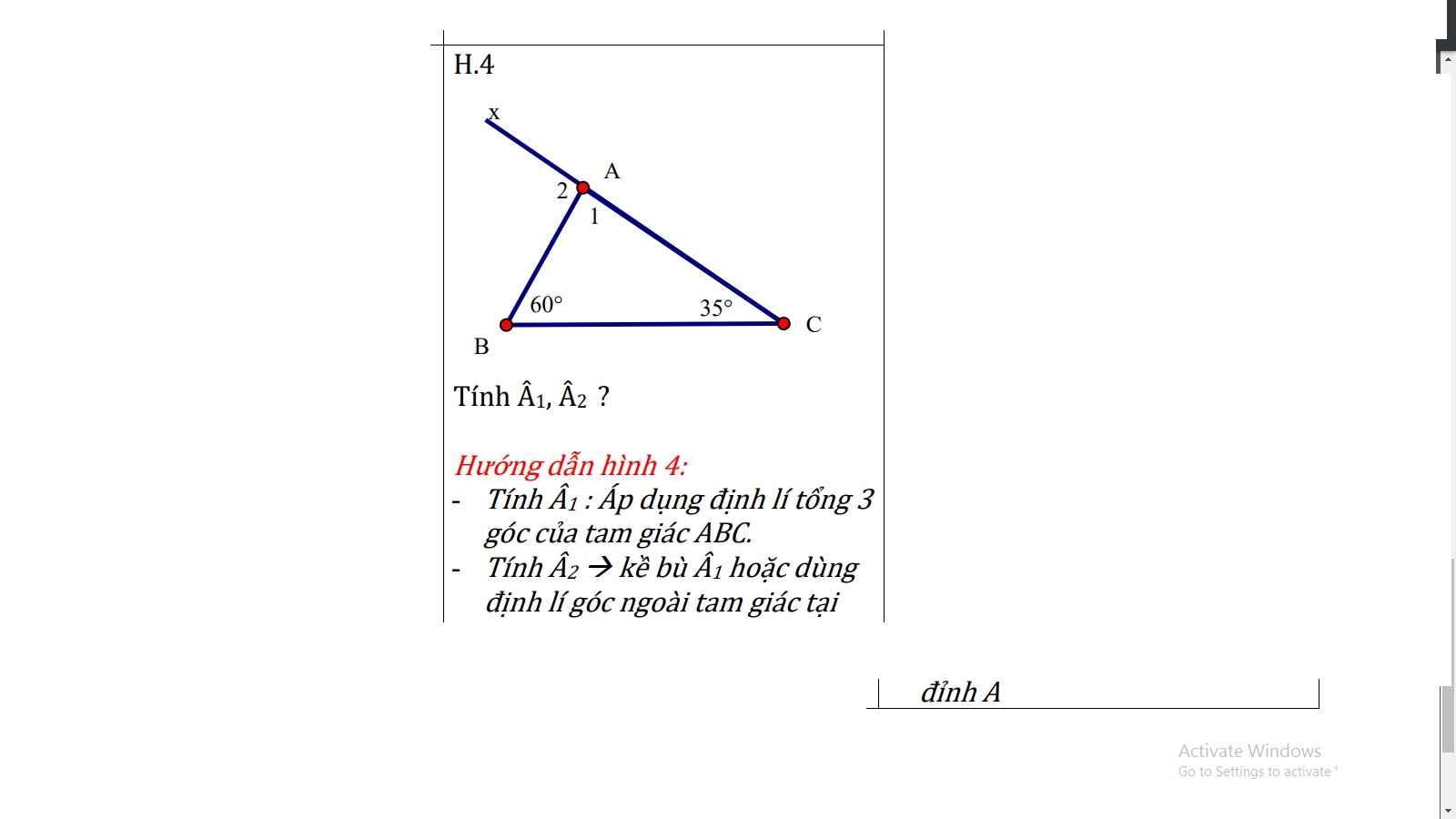


12:
14:
Bài 12: