K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 4 2022
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
5 tháng 9 2021
1: \(\dfrac{4x^3-2x^2-3x+1}{x-2}\)
\(=\dfrac{4x^3-8x^2+6x^2-12x+9x-18+19}{x-2}\)
\(=4x^2+6x+9+\dfrac{19}{x-2}\)
2: \(\dfrac{2x^4-x^3-3x^2-2x}{x-2}\)
\(=\dfrac{2x^4-4x^3+5x^3-10x^2+7x^2-14x+12x-24+24}{x-2}\)
\(=2x^3+5x^2+7x+12+\dfrac{24}{x-2}\)
23 tháng 5 2022
a, ta có A(x)=2x3+7x2+ax+b
=(2x3+2x2+2x)+(5x2+5x+5)+ax-7x+b-5
=2x(x2+x+1)+5(x2+x+1)+(a-7)x+(b-5)
=(x2+x+1)(2x+5)+(a-7)x+(b-5)
ta có: (x2+x+1)(2x+5)⋮B(x)
→để A(x)⋮B(x) thì (a-7)x+(b-5)=0
→\(\left\{{}\begin{matrix}a-7=0\\b-5=0\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\)
vậy ....
mk trình bày hơi tắt xíu
bn cố gắng dịch nhé
13 tháng 11 2021
\(A=-\left(x^2-4x+4\right)-\left(y^2+4y+4\right)+10\\ A=-\left(x-2\right)^2-\left(y+2\right)^2+10\le10\\ A_{max}=10\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-2\end{matrix}\right.\)
MP
1
5 tháng 10 2021
Bài 2:
a: Ta có: \(M=2x\left(2x^3-3x\right)-x^2\left(3x^2-2\right)-x^2\left(x^2-4\right)\)
\(=4x^4-6x^2-3x^4+2x^2-x^4+4x^2\)
=0
b: Ta có: \(N=x\left(y^2-x\right)-y\left(xy-x^2\right)-x\left(xy-x-1\right)\)
\(=xy^2-x^2-xy^2+x^2y-x^2y+x^2+x\)
\(=x\)
30 tháng 7 2023
a: AN+CN=AC
=>AN=20-15=5cm
Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Xét ΔAMN và ΔNPC có
góc AMN=góc NPC(=góc B)
góc ANM=góc NCP)
=>ΔAMN đồng dạng với ΔNPC
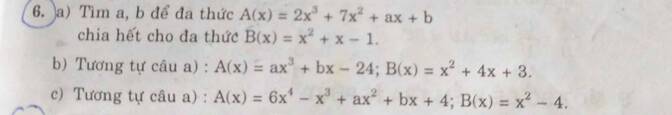
\(x^4-4x^2+x^2-4x=0\)
\(\Leftrightarrow x^2\left(x^2-4\right)+x\left(x-4\right)=0\)
\(\Leftrightarrow x\left(x^3-4x+x-4\right)=0\)
\(\Leftrightarrow x\left(x^3-3x-4\right)=0\)
hay x=0
\(\Leftrightarrow x\left(x^3-3x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^3-3x-4=0\end{matrix}\right.\\ \Leftrightarrow x=0\)