K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 2 2022
Xet tam giac BDC va tam giac CEB ta co
^BDC = ^CEB = 900
BC _ chung
^BCD = ^CBE ( gt )
=> tam giac BDC = tam giac CEB ( ch - gn )
=> ^DBC = ^ECB ( 2 goc tuong ung )
Ta co ^B - ^DBC = ^ABD
^C - ^ECB = ^ACE
=> ^ABD = ^ACE
Xet tam giac IBE va tam giac ICD
^ABD = ^ACE ( cmt )
^BIE = ^CID ( doi dinh )
^BEI = ^IDC = 900
Vay tam giac IBE = tam giac ICD (g.g.g)
c, Do BD vuong AC => BD la duong cao
CE vuong BA => CE la duong cao
ma BD giao CE = I => I la truc tam
=> AI la duong cao thu 3
=> AI vuong BC
BA
1
23 tháng 9 2021
Ta có: \(3x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}\)
\(2y=5z\Rightarrow\dfrac{y}{5}=\dfrac{z}{2}\Rightarrow\dfrac{y}{15}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}=\dfrac{x+z}{20+6}=\dfrac{52}{26}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=20.2=40\\y=15.2=30\\z=6.2=12\end{matrix}\right.\)
15 tháng 9 2021
a) \(\dfrac{1}{4}-3\left(\dfrac{1}{12}+\dfrac{3}{8}\right)=\dfrac{1}{4}-\dfrac{1}{4}-\dfrac{9}{8}=-\dfrac{9}{8}\)
b) \(\left(-\dfrac{2}{3}+\dfrac{3}{5}\right):\dfrac{1}{50}-30=\left(-\dfrac{2}{3}+\dfrac{3}{5}\right).50-30=-\dfrac{100}{3}+30-30=-\dfrac{100}{3}\)
TN
1
10 tháng 1 2022
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
12 tháng 9 2023
Diện tích xung quanh hình hộp chữ nhật là :
\(\left(2,5+1,8\right).2.2=17,2\left(đơn.vị.diện.tích\right)\)
Diện tích toàn phần hình hộp chữ nhật là :
\(17,2+2.2,5.1,8=26,2\left(đơn.vị.diện.tích\right)\)
Đáp số...
12 tháng 9 2023
Bạn xem lại đề về chỗ dài và rộng nha.
Diện tích xung quanh hình hộp chữ nhật là :
\(2.\left(2,5+1,8\right).2=17,2\left(đvdt\right)\)
Diện tích 2 đáy hình hộp chữ nhật đó là :
\(2.2,5.1,8=9\left(đvdt\right)\)
Diện tích toàn phần hình hộp chữ nhật đó là :
\(17,2+9=26,2\left(đvdt\right)\)
Thể tích hình hộp chữ nhật đó là :
\(2,5.1,8.2=9\left(đvdt\right)\)
đs........
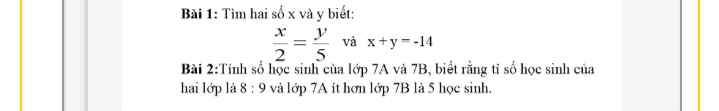
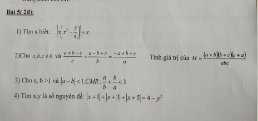
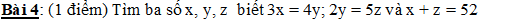
Bài 1:
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{-14}{7}=-2\)
\(\Rightarrow x=2.(-2)=-4; y=5(-2)=-10\)
Bài 2:
Gọi số học sinh lớp 7A, 7B lần lượt là $a,b$. Theo bài ra ta có:
$\frac{a}{8}=\frac{b}{9}$ và $b-a=5$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{b}{9}=\frac{a}{8}=\frac{b-a}{9-8}=\frac{5}{1}=5$
$\Rightarrow b=9.5=45; a=5.8=40$ (học sinh)