
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1)
ĐKXĐ: x>4
Ta có: \(\dfrac{\sqrt{x+5}}{\sqrt{x-4}}=\dfrac{\sqrt{x-2}}{\sqrt{x+3}}\)
\(\Leftrightarrow x^2+8x+15=x^2-6x+8\)
\(\Leftrightarrow8x+6x=8-15\)
\(\Leftrightarrow14x=-7\)
hay \(x=-\dfrac{1}{2}\)(loại)
2) Ta có: \(\sqrt{4x^2-9}=3\sqrt{2x-3}\)
\(\Leftrightarrow\sqrt{2x-3}\left(\sqrt{2x+3}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\2x+3=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\2x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=3\end{matrix}\right.\)

Xét tg ABO và tg ACO có
AO chung
AB=AC (gt)
OB=OC=R
=> tg ABO = tg ACO (c.c.c)
\(\Rightarrow\widehat{ACO}=\widehat{ABO}=90^o\Rightarrow AC\perp OC\) => AC là tiếp tuyến với (O)
b/
Xét tg vuông EOI và tg vuông COI có
OE=OC=R; OI chung => tg EOI = tg COI (hai tg vuông có 2 cạnh góc vuông bằng nhau)
Xét tg vuông EDI và tg vuông CDI có
DI chung
tg EOI = tg COI (cmt) => IE=IC
=> tg EDI = tg CDI (hai tg vuông có 2 cạnh góc vuông bằng nhau)
Xét tg DEO và tg DCO có
DO chung
OE=OC=R
tg EDI = tg CDI (cmt) => DE=DC
=> tg DEO = tg DCO (c.c.c)
\(\Rightarrow\widehat{DEO}=\widehat{DCO}=90^o\Rightarrow DE\perp OE\) => DE là tiếp tuyến với (O, R)

a: ΔOBC cân tại O
mà OA là đường cao
nên OA là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O)
b: Ta có: \(\widehat{KOA}+\widehat{BOA}=\widehat{KOB}=90^0\)
\(\widehat{KAO}+\widehat{COA}=90^0\)(ΔOCA vuông tại C)
mà \(\widehat{BOA}=\widehat{COA}\)
nên \(\widehat{KOA}=\widehat{KAO}\)
=>KA=KO
d: Xét (O) có
\(\widehat{ACI}\) là góc tạo bởi tiếp tuyến CA và dây cung CI
\(\widehat{CDI}\) là góc nội tiếp chắn cung CI
Do đó: \(\widehat{ACI}=\widehat{CDI}\)
ΔOCA vuông tại C
=>\(CO^2+CA^2=OA^2\)
=>\(CA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(CA=R\sqrt{3}\)
Xét ΔACI và ΔADC có
\(\widehat{ACI}=\widehat{ADC}\)
\(\widehat{CAI}\) chung
Do đó: ΔACI đồng dạng với ΔADC
=>\(\dfrac{AC}{AI}=\dfrac{AD}{AC}\)
=>\(AI\cdot AD=AC^2=\left(R\sqrt{3}\right)^2=3R^2\) không đổi

bài 1:
\(\left\{{}\begin{matrix}x+y=57\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+4y=228\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6y=234\\x+y=57\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=39\\x=18\end{matrix}\right.\)

Hướng dẫn:
Ta có:
\(x^2-xy+y^2=2x-3y-2\)
\(\Leftrightarrow2x^2-2xy+2y^2-4x+6y+4+9=9\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-4x+4\right)+\left(y^2+6y+9\right)=9\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-2\right)^2+\left(y+3\right)^2=9\)
Xét....
Đây là 1 cách nhưng làm hơi dài.
\(x^2-xy+y^2=2x-3y-2\\ \Leftrightarrow x^2-xy+y^2-2x+3y+2=0\left(1\right)\\ \Leftrightarrow x^2-x\left(y+2\right)+y^2+3y+2=0\)
Coi đây là pt bậc 2 ẩn x
Ta có: \(\Delta=\left[-\left(y+2\right)\right]^2-4\left(y^2+3y+2\right)=y^2+4y+4-4y^2-12y-8=-3y^2-8y-4\)
Để pt có nghiệm nguyên thì \(\Delta\ge0\Leftrightarrow-3y^2-8y-4\ge0\Leftrightarrow-2\le y\le-\dfrac{2}{3}\)
\(\Leftrightarrow y\in\left\{-2;-1\right\}\)
Thay y=-2 vào (1) ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-2\right)+\left(-2\right)^2-2x+3.\left(-2\right)+2=0\\ \Leftrightarrow x^2+2x+4-2x-6+2=0\\ \Leftrightarrow x^2=0\Leftrightarrow x=0\)
Thay y=-1 vào pt ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-1\right)+\left(-1\right)^2-2x+3.\left(-1\right)+2=0\\ \Leftrightarrow x^2+x+1-2x-3+2=0\\ \Leftrightarrow x^2-x=0\\ \Leftrightarrow x\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(0;-2\right);\left(0;-1\right);\left(1;-1\right)\right\}\)


1: Thay \(x=\dfrac{4-\sqrt{7}}{2}\) vào B, ta được:
\(B=\dfrac{1}{\sqrt{\dfrac{4-\sqrt{7}}{2}}+1}=1:\left(\dfrac{\sqrt{7}-1+2}{2}\right)=1\cdot\dfrac{2}{\sqrt{7}+1}=\dfrac{-1+\sqrt{7}}{3}\)

a: Khi m=-2 thì (d): y=-5x-2
ii: Tọa độ giao điểm của (P) và (d) là:
\(\left\{{}\begin{matrix}2x^2+5x+2=0\\y=2x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{-\dfrac{1}{2};-2\right\}\\y\in\left\{\dfrac{1}{2};8\right\}\end{matrix}\right.\)
Vậy: M(-1/2;1/2); N(-2;8)
\(OM=\sqrt{\left(-\dfrac{1}{2}-0\right)^2+\left(\dfrac{1}{2}-0\right)^2}=\sqrt{\dfrac{1}{4}+\dfrac{1}{4}}=\dfrac{\sqrt{2}}{2}\)
\(ON=\sqrt{\left(-2-0\right)^2+\left(8-0\right)^2}=2\sqrt{17}\)
\(MN=\sqrt{\left(-2+\dfrac{1}{2}\right)^2+\left(8-\dfrac{1}{2}\right)^2}=\sqrt{\dfrac{9}{4}+\dfrac{225}{4}}=\dfrac{3\sqrt{26}}{2}\)
\(P=OM+ON+NM\simeq4,93\left(cm\right)\)
\(S=\sqrt{4,93\cdot\left(4,93-\dfrac{\sqrt{2}}{2}\right)\cdot\left(4.93-2\sqrt{17}\right)\left(4.93-\dfrac{3\sqrt{26}}{2}\right)}=13,7\left(cm^2\right)\)

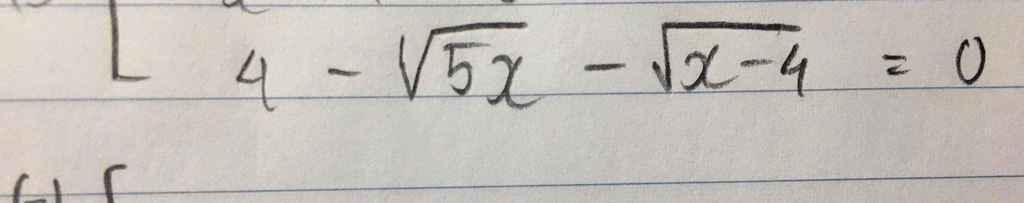

 giải giúp mình với ạa , mình cảm ơn.
giải giúp mình với ạa , mình cảm ơn.


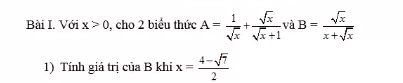

\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
\(\Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)
\(\Leftrightarrow\sqrt{x-2}=10\)
\(\Leftrightarrow x-2=100\)
\(\Leftrightarrow x=102\)