
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Pt \(\Leftrightarrow\left(cos^2x+sin^2x\right)^3-3cos^2x.sin^2x\left(cos^2x+sin^2x\right)=1-2sin^22x\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x=1-2sin^22x\)
\(\Leftrightarrow\dfrac{5}{4}sin^22x=0\)\(\Leftrightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}\) \(\left(k\in Z\right)\)
Vậy...






c.
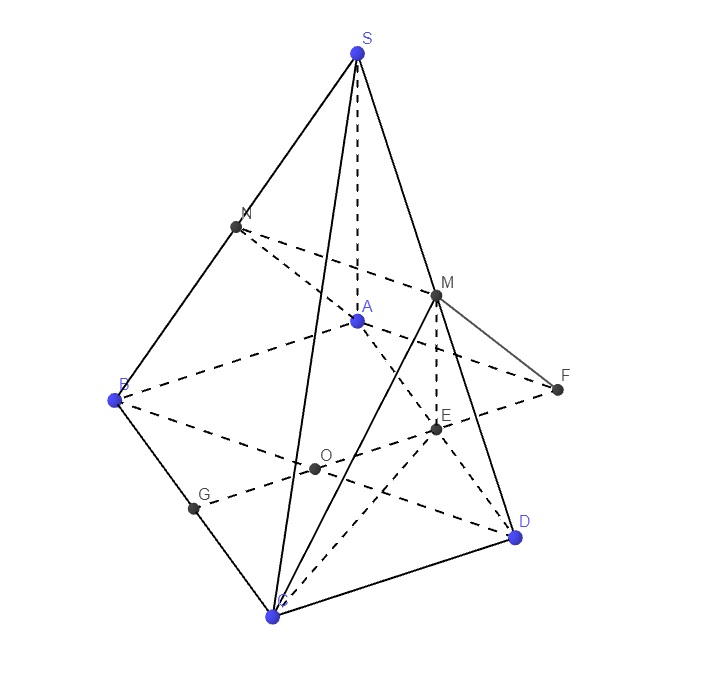
Gọi E là trung điểm AD \(\Rightarrow EM\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}EM=\dfrac{1}{2}SA=a\\EM||SA\Rightarrow EM\perp\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow EC\) là hình chiếu vuông góc của CM lên (ABCD)
\(\Rightarrow\widehat{MCE}\) là góc giữa SM và (ABCD)
\(ED=\dfrac{1}{2}AD=a\Rightarrow EC=\sqrt{CD^2+ED^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{MCE}=\dfrac{EM}{EC}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{MCE}=...\)
e.
Gọi O là trung điểm BD, qua A kẻ đường thẳng song song BD cắt OE kéo dài tại F
\(\Rightarrow ABOF\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow\left\{{}\begin{matrix}AF=OB=\dfrac{1}{2}BD\\AF||BD\end{matrix}\right.\)
Lại có MN là đường trung bình tam giác SBD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}MN=AF\\MN||AF\end{matrix}\right.\) \(\Rightarrow ANMF\) là hình bình hành
\(\Rightarrow AN||MF\Rightarrow\left(AN;CM\right)=\left(AN;MF\right)=\widehat{CMF}\) nếu nó ko tù hoặc bằng góc bù của nó nếu \(\widehat{CMF}\) là góc tù
Ta có: \(MF=AN=\dfrac{a\sqrt{5}}{2}\) ; \(CM=\sqrt{CE^2+EM^2}=a\sqrt{3}\)
ABOF là hình bình hành nên AODF cũng là hình bình hành \(\Rightarrow E\) là tâm hình bình hành
\(\Rightarrow EF=OF=\dfrac{AB}{2}=\dfrac{a}{2}\)
Gọi G là giao điểm OE và BC \(\Rightarrow FG=EG+EF=a+\dfrac{a}{2}=\dfrac{3a}{2}\)
\(\Rightarrow CF=\sqrt{FG^2+CG^2}=\dfrac{a\sqrt{13}}{2}\)
ĐỊnh lý hàm cos:
\(cos\widehat{CMF}=\dfrac{CM^2+MF^2-CF^2}{2CM.MF}=\dfrac{\sqrt{15}}{15}\Rightarrow\widehat{CMF}\)

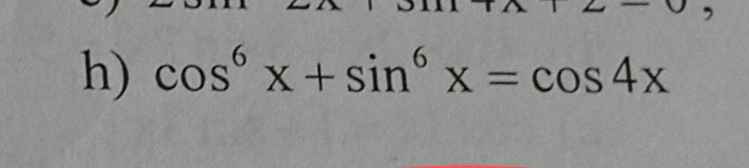 giai chi tiết giúp e với!!!
giai chi tiết giúp e với!!!






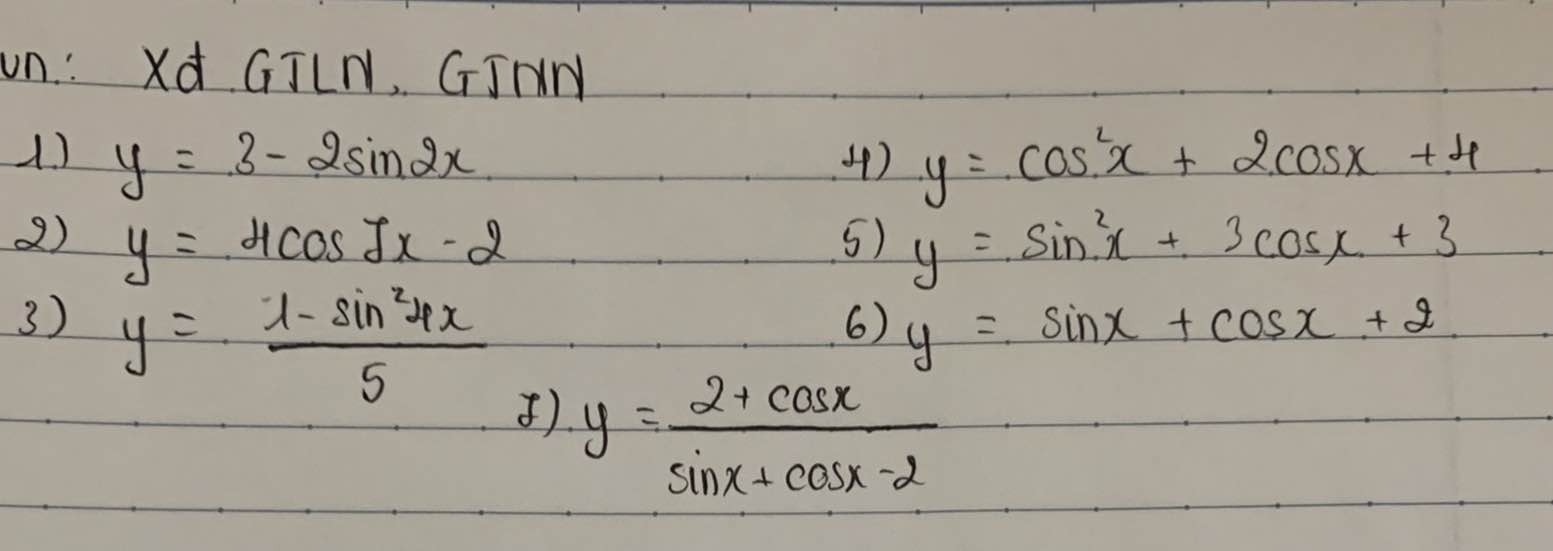

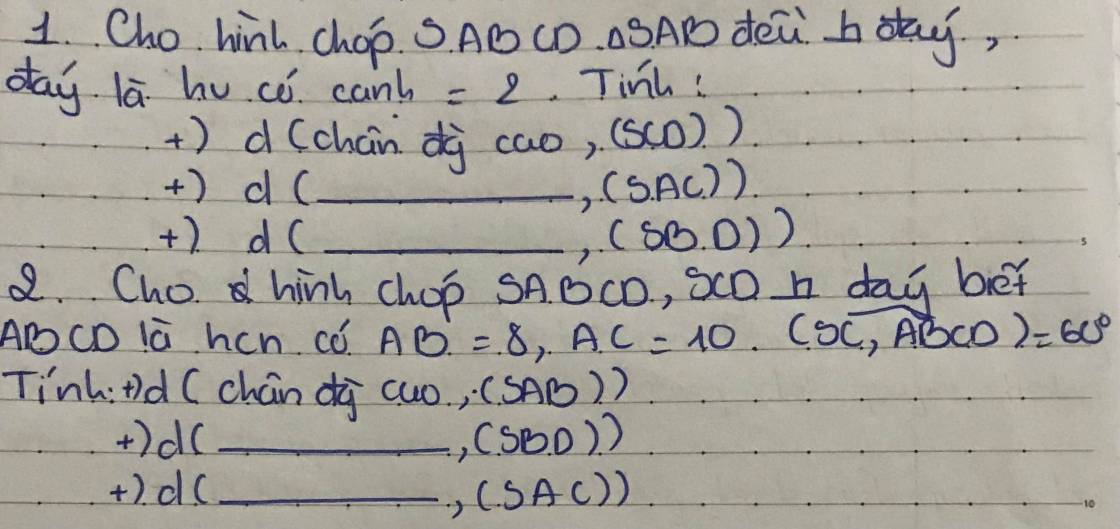
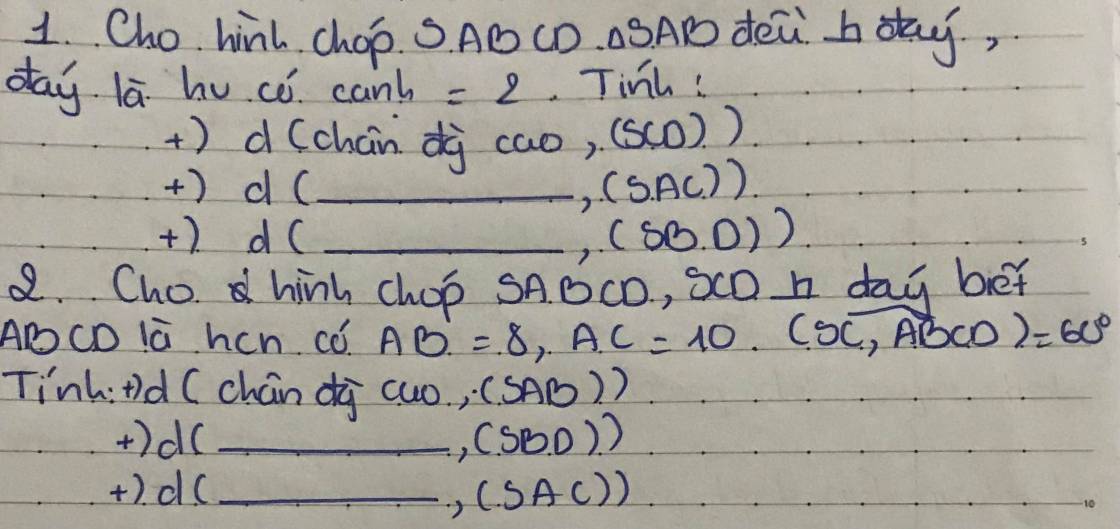

Bài 10
ĐKXĐ: \(\left\{{}\begin{matrix}cos\left(1-x\right)\ne0\\2sin2x.cos2x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}cos\left(1-x\right)\ne0\\sin4x\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-x\ne\dfrac{\pi}{2}+k\pi\\4x\ne\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne1-\dfrac{\pi}{2}-k\pi\\x\ne\dfrac{\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.\left(k\in Z\right)\)
Bài 11.
ĐKXĐ: \(\left\{{}\begin{matrix}cos^2x-sin^2x\ne0\\sin2x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}cos2x\ne0\\sin2x\ne0\end{matrix}\right.\)
\(\Leftrightarrow2x\ne\dfrac{k\pi}{4}\Leftrightarrow x\ne\dfrac{k\pi}{8}\)
Bài 12.
ĐKXĐ: \(\left\{{}\begin{matrix}1-2cos^2x\ne0\\1+tanx\ne0\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}cos2x\ne0\\tanx\ne-1\\cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ne\dfrac{\pi}{2}+k\pi\\x\ne-\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x\ne-\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\left(k\in Z\right)\)
Bài 10:
ĐKXĐ của hàm số \(y=\dfrac{tan\left(1-x\right)+2}{2sin2xcos2x-1}\) là:
\(\left\{{}\begin{matrix}1-x\ne\dfrac{\pi}{2}+k\pi\\2sin2xcos2x-1\ne0\end{matrix}\right.,k\inℤ\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne1-\dfrac{\pi}{2}+k\pi\\sin4x\ne1\end{matrix}\right.,k\inℤ}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne1-\dfrac{\pi}{2}+k\pi\\4x\ne\dfrac{\pi}{2}+k2\pi\end{matrix}\right.,k\inℤ\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne1-\dfrac{\pi}{2}+k\pi\\x\ne\dfrac{\pi}{8}+\dfrac{k\pi}{2}\end{matrix}\right.,k\inℤ\)