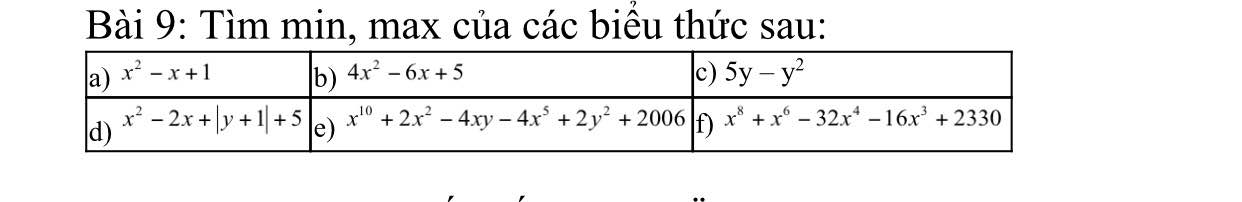K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
Nguyễn Đức Trí
VIP
20 tháng 7 2023
\(...\Rightarrow x^3-9x^2+27x-27-\left(x^3-27\right)+9\left(x^2+2x+1\right)=15\)
\(\Rightarrow x^3-9x^2+27x-27-x^3+27+9x^2+18x+9=15\)
\(\Rightarrow45x+9=15\Rightarrow45x=6\Rightarrow x=\dfrac{6}{45}=\dfrac{2}{15}\)
LM
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
0
27 tháng 7 2021
Ta có: \(2x^2y\cdot\left(x^3y+4x^3y-4x-x^2y+5x^3y-y\right)\)
\(=2x^2y\cdot\left(10x^3y-4x-x^2y-y\right)\)
\(=20x^5y^2-8x^3y-2x^4y^2-2x^2y^2\)
29 tháng 6 2016
x^3-6x^2+12x-8=0
-> x^3-2x^2-4x^2+8x+4x-8=0
-> x^2(x-2)-4x(x-2)+4(x-2)=0
-> (x-2)(x^2-4x+4)=0
->(x-2)(x-2)^2=0
-> (x-2)^3=0
->x-2=0
-> x=2 .
29 tháng 6 2016
x^3-6x^2+12x-8=0
-> x^3-2x^2-4x^2+8x+4x-8=0
-> x^2(x-2)-4x(x-2)+4(x-2)=0
-> (x-2)(x^2-4x+4)=0
->(x-2)(x-2)^2=0
-> (x-2)^3=0
->x-2=0
-> x=2 .
nha ><
26 tháng 5 2022
a,
Xét Δ ABH và Δ CBA, có :
\(\widehat{ABH}=\widehat{CAB}\) (góc chung)
\(\widehat{AHB}=\widehat{CAB}=90^o\)
=> Δ ABH ~ Δ CBA (g.g)
=> \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)
=> \(AB^2=BH.BC\)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+AC^2\) (Py - ta - go)
=> \(BC^2=15^2+20^2\)
=> BC = 25 (cm)
Ta có : \(AB^2=BH.BC\) (cmt)
=> \(15^2=BH.25\)
=> BH = 9 (cm)
Ta có : BC = BH + CH
=> 25 = 9 + CH
=> CH = 16 (cm)
26 tháng 5 2022
b,
Xét Δ AMN và Δ ACB, có :
\(\widehat{MAN}=\widehat{CAB}=90^o\)
\(\widehat{MAN}=\widehat{CAB}\) (góc chung)
=> Δ AMN ~ Δ ACB (g.g)
=> \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> AM.AB = AN.AC
Ta có : \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> \(\dfrac{AB}{AC}=\dfrac{AN}{AM}\)
=> \(\dfrac{AN}{AM}=\dfrac{15}{20}=\dfrac{3}{4}\)
Vậy : ta có kết luận : Δ AMN = \(\dfrac{3}{4}\) Δ ACB
28 tháng 8 2021
a: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
d: Ta có: \(x^2-2x+\left|y+1\right|+5\)
\(=\left(x-1\right)^2+\left|y+1\right|+4\ge4\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=-1
8 tháng 7 2018
không nhé
(2x+1)(4x^2-xy+1)-(8x^3-1)
= ((2x)^3 -1) - ( 8x^3 - 1 ) = 0
Vậy là không phụ thuộc vào biến nhé bạn