
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(b,\sqrt{9.\left(x-2\right)^2}=18\)
\(\Leftrightarrow3\left|x-2\right|=18\)
\(\Leftrightarrow\left|x-2\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=6\\x-2=-6\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-4\end{matrix}\right.\)
Vậy: \(S=\left\{8;-4\right\}\)

a: Xét (O) có
OI là một phần đường kính
DE là dây
I là trung điểm của DE
DO đó; OI⊥DE
Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=180^0\)
nên A,B,O,C cùng thuộc đường tròn(1)
Xét tứ giác OIAC có \(\widehat{OIA}+\widehat{OCA}=180^0\)
nên OIAC là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra A,I,O,B,C cùng thuộc đường tròn
b: Xét ΔABD và ΔAEB có
\(\widehat{ABD}=\widehat{AEB}\)
\(\widehat{BAD}\) chung
Do đó:ΔABD∼ΔAEB
Suy ra: AB/AE=AD/AB
hay \(AB^2=AD\cdot AE\)
Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(3)
Ta có: OB=OC
nên O nằm tren đường trung trực của BC(4)
Từ (3) và (4) suy ra OA⊥BC

\(=4-\dfrac{12}{5}\sqrt{5}-6+\dfrac{18}{5}\sqrt{5}+2\sqrt{5}-6\)
\(=-8+\dfrac{16}{5}\sqrt{5}\)

a) \(=\left|\sqrt{3}-3\right|+\sqrt{\left(\sqrt{3}-1\right)^2}=3-\sqrt{3}+\sqrt{3}-1=2\)
b) \(=\dfrac{\sqrt{5}+2}{5-4}-\dfrac{\sqrt{5}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{5}+2-\sqrt{5}=2\)

\(M=\dfrac{3}{2}\cdot4\sqrt{2x}-\dfrac{1}{3}\cdot3\sqrt{2x}+\dfrac{2}{5}\cdot5\sqrt{2x}-4\sqrt{2x}=6\sqrt{2x}-\sqrt{2x}+2\sqrt{2x}-4\sqrt{2x}=3\sqrt{2x}\)

a: Để Δ//d1 thì \(\left\{{}\begin{matrix}m^2-2=2\\m-1\ne-3\end{matrix}\right.\Leftrightarrow m=2\)

a: a*c=-3m^2<=0
=>Phương trình luôn có hai nghiệm
b: Khi x=-3 thì (1) sẽ là;
(-3)^2+6(2m-1)-3m^2=0
=>-3m^2+9+12m-6=0
=>-3m^2+12m+3=0
=>\(m=2\pm\sqrt{5}\)


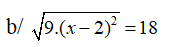



Lời giải:
a.
b. PT hoành độ giao điểm:
$-2x+4=3x-1$
$\Leftrightarrow x=1$
$y=3x-1=3.1-1=2$
Vậy $A(1;2)$